PyTorch: podział zbioru, transformacje, uczenie na GPU oraz wizualizacja metryki

Dziś taki lekki misz-masz. W uczeniu maszynowym określenie struktury modelu i trening sieci neuronowej to stosunkowo niewielkie elementy dłuższego łańcucha czynności, który rozpoczyna się od załadowania zbioru danych, jego podziału na podzbiory uczący, walidacyjny oraz testowy i odpowiedniego serwowania danych do modelu. Po drodze pojawiają się również takie kwestie jak transformacja danych, uczenie na GPU oraz zbieranie metryk i ich wizualizacja, w celu określenia skuteczności naszego modelu. W niniejszym poście chciałbym skupić się nie tyle na architekturze modelu i na samym uczeniu, co właśnie na tych kilku czynnościach, które często wymagają od nas całkiem sporo czasu i wysiłku. Do kodowania wykorzystana zostanie moja ulubiona biblioteka PyTorch.

Z niniejszego posta dowiesz się między innymi:

• Jak można podzielić zbiór danych na uczący, walidacyjny i testowy?
• Jak dokonać transformacji zbioru, np. znormalizować dane i co jeżeli potrzebujesz odwrócić proces normalizacji?
• W jaki sposób w PyTorch wykorzystać GPU?
• Jak wyliczać najpopularniejszą metrykę, czyli accuracy, dla pętli uczącej, walidacyjnej i testowej?

Załadowanie i transformacje zbioru

Na początku trochę „formalności”, czyli niezbędne importy z krótkimi wyjaśnieniami w komentarzach dlaczego i po co.

# main libraries
import torch
import torchvision

# All datasets in torchvision.dataset are subclasses
# of torch.utils.data.Dataset, thus we may use MNIST directly in DataLoader
from torchvision.datasets import CIFAR10
from torch.utils.data import DataLoader

# an optimizer and a loss function
from torch.optim import Adam
from torch.nn import CrossEntropyLoss

# required for creating a model
from torch.nn import Conv2d, BatchNorm2d, MaxPool2d, Linear, Dropout
import torch.nn.functional as F

# tools and helpers
import numpy as np
from timeit import default_timer as timer
import matplotlib.pyplot as plt
from torch.utils.data import random_split
from torchvision import transforms
import matplotlib.pyplot as plt

Korzystamy z pakietu torchvision, który oferuje klasy do ładowania najpopularniejszych zbiorów danych, na których najprościej eksperymentować. Klasa ładująca zbiór CIFAR10, którą zaraz zastosujemy, jako jeden z parametrów przyjmuje obiekt klasy torchvision.transforms. Umożliwia on wykonanie na ładowanym zbiorze szeregu transformacji takich jak zamiana danych na tensory, normalizacja, dodanie paddingów, wycinanie fragmentów obrazu, obroty, transformacje perspektywy, itp. Przydają się one zarówno w prostych przypadkach, jak i w bardziej skomplikowanych, gdy np. chcemy wykonać data augmentation. Dodatkowo transformacje można serializować, używając torchvision.transforms.Compose.

My potrzebujemy jedynie przekształcić dane do tensora i znormalizować je, stąd:

Trzy uwagi do powyższego:

• mean i std to wyliczone wartości średnie oraz ich odchylenie standardowe dla każdego z kanałów obrazka,
• jak widać definiujemy transformatę osobno dla zbioru uczącego i testowego. Są one takie same, bo nie stosujemy dla zbioru uczącego data augmentation. Teoretycznie więc można było zastosować jedną transformatę w obu przypadkach, ale dla jasności, jak również na wypadek gdybyśmy potem chcieli to jednak zmienić, zostawiamy obie transformaty oddzielnie,
• wartości mean i std przydadzą się nam do późniejszej de-normalizacji na potrzeby wyświetlania przykładowych obrazków, bo po normalizacji przestaną one być czytelne dla ludzkiego oka.

Mając transformaty, możemy załadować zbiory. Klasa CIFAR10 jest podklasą torch.utils.data.Dataset, o której szerzej pisałem w tym wpisie.

Denormalizacja i wyświetlenie

Dobrą praktyką jest podejrzenie przykładowych elementów ze zbioru uczącego. Problemem jest jednak to, że zostały one znormalizowane, czyli wartości poszczególnych pikseli zostały zmienione oraz przekształcone do tensora, co z kolei zmieniło kolejność kanałów obrazka. Poniżej klasa de-normalizująca i przywracająca pierwotny kształt.

Potrzebujemy jeszcze słownika, który tłumaczyłby numery klas na ich nazwy, zgodnie z definicją zbioru CIFAR10, a także funkcji wyświetlającej kilka losowo wybranych obrazków.

No to przyjrzymy się kilku elementom tego zbioru …

Podział zbioru na uczący, testowy i walidacyjny

Należy zauważyć, że konstruktor zbioru CIFAR10 umożliwia pobranie albo zbioru uczącego, albo testowego. Co jednak, jeśli chcemy wydzielić jeszcze zbiór walidacyjny, który pozwoli nam określić skuteczność w trakcie uczenia? Musimy samodzielnie wydzielić go z ze zbioru uczącego. Pomocna w tym zakresie będzie funkcja random_split z pakietu torch.utils.data.

Mając trzy obiekty klasy Dataset: train_dataset, validation_dataset i test_dataset możemy zdefiniować DataLoadery, które umożliwią serwowanie danych w batchach.

Architektura modelu

Aby nie skupiać się zbytnio na architekturze sieci, którą chcemy zastosować – bo nie taki jest cel niniejszego posta – wykorzystamy sieć zaprojektowaną w tym wpisie na temat konwolucyjnych sieci neuronowych. Warto jednak w tym miejscu zauważyć, że jednym z zagadnień przy projektowaniu sieci jest wymiarowanie danych. Aby sprawdzić wielkość wektora wejściowego, jaki będzie serwowany przez DataLoader, można wykonać następujący kod:

Przenosimy się na GPU i wyliczamy accuracy

Uczenie nieco bardziej rozbudowanej sieci neuronowej na CPU nie ma większego sensu. Prosty test jaki przeprowadziłem na Google Colab pokazał, że przejście jednej epoki na CPU zajmuje około 2600 sekund, gdy tymczasem na GPU to samo zajęło 66 sekund. Te czasy w oczywisty sposób zależą od wielu czynników, na które nie mamy wpływu, jak choćby na jakie maszyny skieruje nas silnik Google Colab, ale wnioski zawsze będą podobne – uczenie na GPU może być kilkadziesiąt razy szybsze.

Jak zatem najprościej przesiąść się w PyTorch z CPU na GPU? Oczywiście w Google Colab musimy wykonać Runtime->Change runtime type i zmienić środowisko wykonawcze na GPU. Ale główne zmiany należy wykonać w kodzie. Na szczęście nie ma ich dużo i są one dość proste.

Sprawa zasadnicza to ustalenie z jakim środowiskiem mamy do czynienia. Poniższy fragment kodu jest powszechnie stosowaną dobrą praktyką.

W następnym kroku tworzymy model i przenosimy go na aktualnie dostępne urządzenie.

Każde uczenie musi mieć zdefiniowane kilka parametrów oraz wskazanie użytych narzędzi. Poniżej określamy ilość epok, learning_rate oraz optimizer, jak również sposób liczenia błędu. Pojawiają się również po raz pierwszy dwie listy, w których w każdej epoce będziemy zapisywali accuracy. Umożliwi to nam potem narysowanie ładnego wykresu.

Poniższy kod to główna pętla ucząca. Dzieje się tu kilka rzeczy, które nas mogą interesować w kontekście niniejszego posta, więc do niektórych linii przypisałem indeksy, które krótko skomentuję:

(1) – będziemy mierzyli czas uczenia.
(2) – dobrą praktyką jest sygnalizowanie silnikowi PyTorch kiedy następuje uczenie, a kiedy jedynie ewaluacja na zbiorze walidacyjnym lub testowym. Istotnie poprawia to wydajność części ewaluacyjnych.
(3) – przenosimy dane (batch) na GPU. 
(4) – wartość, którą otrzymujemy po przepuszczeniu danej wejściowej przez sieć (tu: yhat) to tzw. logits, czyli wartości teoretycznie z przedziału od plus do minus nieskończoności. Target zawiera liczby od 0 do 9 wskazujące na właściwą klasę. Funkcja obliczająca błąd sieci (tu: CrossEntropyLoss) wewnętrznie radzi sobie z odpowiednim porównaniem tych wartości. My jednak obliczając accuracy – w punkcie (5) – musimy najpierw samodzielnie obliczyć odpowiedź sieci. Używamy do tego funkcji argmax, która zwraca indeks, w którym występuje najsilniejsza (największa co do wartości) odpowiedź sieci. Indeks ten będzie jednocześnie numerem klasy, do której sieć przypisała wartość wejściową. W ten sposób otrzymujemy prediction – wektor zawierający przypisanie klasy dla każdego elementu aktualnie przetwarzanego batcha.
(5) – do wyliczenia accuracy bazującej na danych w dwóch wektorach y i prediction najwygodniej użyć biblioteki numpy, która świetnie radzi sobie z wektoryzacją operacji. Aby dane, które znajdują się na GPU trafiły ostatecznie do listy przetwarzanej w środowisku CPU musimy użyć .detach().cpu().numpy().
(6) – dla każdej epoki uczenia przetwarzamy zbiór walidacyjny i wyliczamy dla niego accuracy, aby porównać z accuracy wyliczoną dla zbioru uczącego. Na tej podstawie będziemy widzieli czy proces uczenia wpadł w overfitting czy nie.

W efekcie uczenia na 40 epokach otrzymujemy następujące wyniki:

>>> Epoch #1. Train accuracy: 34.20. Validation accuracy: 47.32
>>> Epoch #2. Train accuracy: 51.58. Validation accuracy: 57.00
>>> Epoch #3. Train accuracy: 58.11. Validation accuracy: 61.56
>>> Epoch #4. Train accuracy: 62.18. Validation accuracy: 64.16
................................................................
>>> Epoch #38. Train accuracy: 90.86. Validation accuracy: 73.86
>>> Epoch #39. Train accuracy: 91.42. Validation accuracy: 73.30
>>> Epoch #40. Train accuracy: 91.68. Validation accuracy: 73.40

Jak widać różnica między accuracy na zbiorze uczącym (91%) a zbiorze walidacyjnym (73%) jest spora. Model wpadł w overfitting, co bardzo dobrze pokazuje zresztą poniższy wykres.

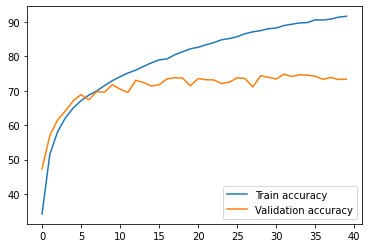
Problem overfittingu jest istotny i jest kilka metod, które można zastosować, aby go zmniejszyć. Część została zresztą zaaplikowana do powyższego modelu (np. warstwa Dropout). Więcej o zapobieganiu overfittingowi w tym poście.

Na koniec procesu uczenia sprawdzamy jak model radzi sobie na zbiorze testowym, czyli danych, których model nie widział podczas uczenia.

Podsumowanie

Niniejszy post miał charakter narzędziowy. Skupiliśmy się na kilku obszarach, które są czasami trudniejsze technicznie niż sam proces budowania architektury modelu. Zobaczyliśmy w jaki sposób można załadować zbiór i podzielić go na trzy podzbiory: uczący, walidacyjny i testowy. Pobieżnie przyjrzeliśmy się transformacjom jakich można dokonywać korzystając z klasy transforms oraz w jaki sposób można wyświetlić obrazki ze zbioru uczącego, odwracając uprzednio transformację. Po krótkim przystanku przy wymiarowaniu sieci nasza uwaga przeniosła się na uczenie w środowisku GPU oraz wyliczenie accuracy. Uzyskany efekt: 72% trafności na zbiorze testowym to nie jest zbyt dobry wynik dla zbioru CIFAR10, ale nie to było celem posta. Osobom zainteresowanym podniesieniem efektywności uczenia polecam post dotyczący data augmentation. Wprawdzie wykorzystuje on framework Keras, ale PyTorch również oferuje narzędzia do wykonania analogicznych operacji. Bardziej zresztą istotna jest sama idea stojąca za serwowaniem do uczenia sztucznie modyfikowanych danych niż użyta biblioteka. 

Całość skryptu dostępna w moim repo na githubie.