W momencie pisania tego posta (kwiecień 2023) nadal panuje dość powszechna ekscytacja możliwościami dużych modeli językowych. Możliwości te w spektakularny sposób pokazało nam rozwiązanie udostępnione pod koniec 2022 przez OpenAI i nasz świat nigdy nie będzie już taki sam. Duże modele językowe, w tym konwersacyjne takie jak ChatGPT, w większości wykorzystują wariacje architektury Transformer. Punktem odniesienia w tym zakresie jest przełomowy artykuł naukowy inżynierów Google z 2017: „Attention is all you need„1, w którym zaproponowano wykorzystanie wariantu architektury encoder-decoder, w połączeniu z tzw. mechanizmem self-attention i kilkoma sprytnymi trikami, w celu zbudowania modelu, który będzie efektywnie tłumaczył z jednego języka na drugi. Model ten nazwano Transformer i mimo że na początku nie wydawał się on przełomowy, to w ciągu kilku lat zdobył szturmem nie tylko domenę NLP, ale również przetwarzania obrazów. W niniejszym wpisie chciałbym pokazać jak można zbudować na bazie tej koncepcji mały model językowy, który wytrenowany na XIX-wiecznej klasycznej literaturze – konkretnie na „Potopie” Henryka Sienkiewicza – można wykorzystać do wygenerowania tekstów, stylem przypominających tekst źródłowy.
Post powstał głównie na bazie moich eksperymentów z kodowaniem relatywnie prostych modeli językowych. Jest oparty na części architektury Transformer i zainspirowany serią tutoriali Andreja Karpathy’ego2. Jest skierowany do osób mających już jakąś podstawową wiedzę w temacie NLP oraz warsztat narzędziowy obejmujący Pythona i bibliotekę Pytorch. Raczej nie da się wszystkiego o czym należałoby napisać zmieścić w jednym poście. Powstały więc trzy części i ostatecznie coś na kształt małego tutoriala, z możliwością samodzielnego tworzenia części kodu. Przy okazji: na blogu jest dostępny inny, w mojej mocno subiektywnej opinii 😉 całkiem dobry, tutorial o sieciach konwolucyjnych. Gdyby ktoś chciał poznać CNN od podszewki, to tu jest pierwsza część tego tutoriala.
Podsumowując, w części pierwszej:
– spojrzymy z lotu ptaka na klasyczną architekturą Transformer oraz ustalimy co z niej dla siebie wytniemy,
– stworzymy klasę implementującą feed forward neural network – klasa ta zostanie potem wykorzystana przy budowie modelu,
– wykonamy prostą implementację mechanizmu self-attention, przy okazji ustalimy po co i jak maskujemy przyszłość w decoderze,
– stworzymy klasę implementującą masked self-attention – również tę klasę wykorzystamy potem przy budowie naszego generatora tekstu.
W części drugiej:
– zaimplementujemy klasę realizującą multi-head masked self-attention,
– przygotujemy zbiór uczący dla modelu – jak wspomniałem będzie on bazował na treści „Potopu”,
– na chwilę skupimy naszą uwagę na character / word embeddings i jak to się przekłada na nasz model,
– zbudujemy główną klasę modelu, aby spiąć wszystko w całość.
Cześć trzecia to:
– wytworzenie głównej pętli uczącej,
– dodanie walidacji i zapisywania modelu do pliku,
– wyuczenie modelu w Google Colab,
– wykorzystanie wyuczonego modelu do wygenerowania mocno bełkotliwej kontynuacji „Potopu”, plus obśmianie wyników.
Ostatnia kwestia: kod będzie osadzany w treści ale dostępny również na GitHubie. Posty będę jednak pisał w taki sposób, że warto samemu spróbować implementować kod. Wiem z doświadczenia, że tworzenie kodu implementującego czyjś pomysł to nie jest łatwa sprawa, ale czas poświęcony na samodzielne, nawet jeśli ostatecznie nie do końca udane, kodowanie zwróci się w dwójnasób. Do implementacji można wykorzystać środowisko Google Colab lub dowolne inne, najlepiej z dostępnym GPU.
„Zawszem mówił, że gorzałka jeno tęgiej głowie służy.” – Zagłoba
Spójrzmy zatem na trzeźwo na architekturę Transformer i zastanówmy się co z niej można wziąć, aby osiągnąć swój cel, ale też aby dało się to jakoś „przełknąć” w krótkim tutorialu. Z lotu ptaka klasyczny Transformer składa się z dwóch elementów: encodera i decodera. Encoder przyjmuje tekst do tłumaczenia, generuje z niego wewnętrzną reprezentację (na rysunku 1 nazwałem ją sobie „encoded features”) wykorzystując mechanizm self-attention oraz klasyczną sieć neuronową i przekazuje ją decoderowi. Decoder otrzymuje input z encodera i będąc modelem auto-regresywnym konsumuje również output swojego poprzedniego kroku. Stąd na rysunku widać, że inputem do decodera jest również wynik tłumaczenia „przesunięty w prawo”. To budzące czasami wątpliwości „shifted right” oznacza po prostu, że decoder przewidując token w kroku T, pobiera jako input stan tłumaczenia z kroku T-1.
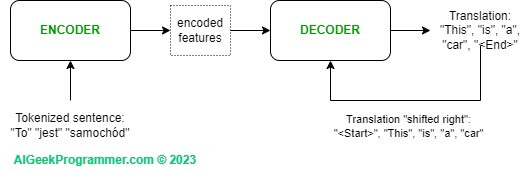
Zarówno encoder jak i decoder składają się z N podbloków. Liczba N jest tutaj uznaniowa i ilość podbloków może być różna. W oryginalnym artykule N było równe 6. Podbloki w encoderze i decoderze nieco się od siebie różnią i najlepiej widać to na rysunku nr 2:
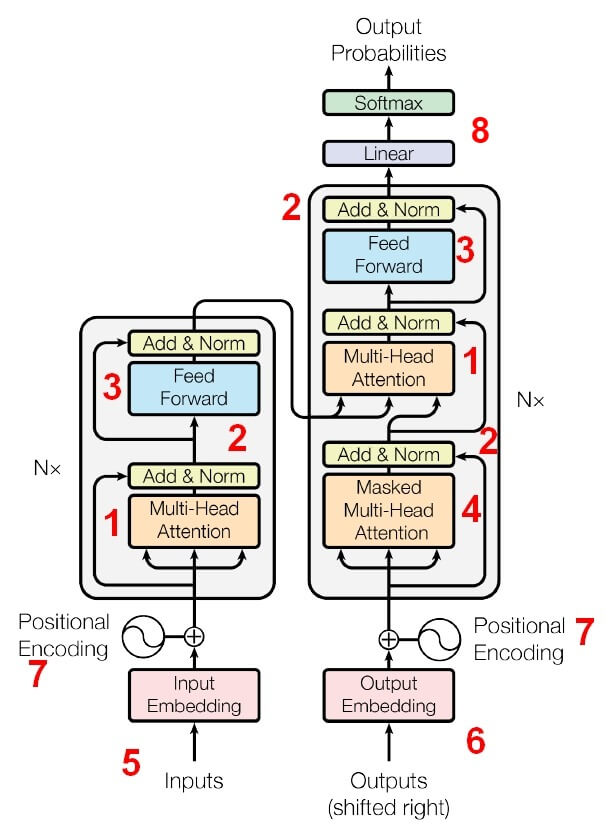
OK, to co mamy ciekawego w tej architekturze…
a) Najciekawszym elementem jest Multi-Head (Self) Attention (1). Przyjrzymy się mu za chwilę w szczegółach. W ogólności self-attention umożliwia identyfikację zależności między wyrazami w tłumaczonym zdaniu. Coś co doskonale robiły Recurrent Neural Network, ale ze względu na sekwencyjność przetwarzania danych w RNNs, w praktyce nie były one możliwe do wykorzystania na bardzo dużych zbiorach danych. Moduł Self-Attention ma możliwość przetwarzania danych wysoce równolegle i opiera się na masowym mnożeniu macierzy, z czym doskonale radzą sobie dedykowane układy GPU. Warto zwrócić uwagę, że Multi-Head Attention ma w tej architekturze swoją nieco bardziej skomplikowaną „siostrę” Masked Multi-Head Attention (4). Czemu i jak maskujemy w decoderze o tym również w dalszej części posta.
b) Na rysunku w kilku miejscach mamy element Add & Norm (2). Add odnosi się tu do tzw. skip-connection. Informacja przepływa tym połączeniem do przodu, omijając blok self-attention, a w drugą stronę swobodnie płynie gradient w procesie optymalizacji. Norm odnosi się do warstwy Layer Normalization (LN), która normalizuje wszystkie dane wejściowe w ramach jednego wektora, a więc niejako normalizacja przebiega w poziomie. Warto tu zaznaczyć, że LN działa inaczej niż Batch Normalization (BN). BN normalizuje jedną zmienną wejściową wzdłuż całego batcha danych, więc niejako pionowo. Gdyby ktoś chciał to lepiej zrozumieć tu znajdzie dobre wytłumaczenie różnicy między LN i BN. Pytorch oferuje implementację LN, więc dodanie jej do modelu będzie relatywnie proste.
c) W dalszej kolejności na diagramie znajdujemy zwykłą gęsto połączoną sieć neuronową, opisaną jaką „Feed Forward” (3). Po wyjściu z decodera mamy liniowe przekształcenie (8), które po prostu zmienia sygnał wyjściowy z decodera do oczekiwanego rozmiaru. Tym rozmiarem jest rozmiar słownika naszego modelu, bo ostatecznie model generuje rozkład prawdopodobieństwa i możemy z niego pobrać najbardziej prawdopodobne następne słowo lub część słowa. Tak! Ostatecznie wszystkie modele językowe, nawet te największe z setkami miliardów parametrów, na wyjściu generują rozkład prawdopodobieństwa, z którego można pobrać najbardziej prawdopodobne następne słowo lub grupę najbardziej prawdopodobnych słów. Swoją drogą, ciekawe czy nasz mózg, kiedy rozmawiamy, również stara się przewidzieć najbardziej prawdopodobne następne słowo? Hmmm… 😉
d) Ostatnią częścią modelu są dane wejściowe. Do encodera trafia ciąg wyrazów (np. zdanie do przetłumaczenia). Dokonywany jest tzw. word embedding, który jest przekształceniem każdego wyrazu (lub części wyrazu, bo nie zawsze całe wyrazy stają się tokenami – zależy to od rodzaju użytego embeddingu) do jego reprezentacji cyfrowej (5). Następnie dodawane są informacje o pozycjach wyrazów w zdaniu – „Positional Encoding” (7). Jest to istotne dla modelu z dwóch powodów. Po pierwsze, w przypadku modelu tłumaczącego między językami, informacja o kolejności wyrazów w języku A jest istotna dla wygenerowania tłumaczenia w języku B, bo języki zwykle mają różną konstrukcję składniową (różne części mowy występują w różnych miejscach). Drugi powód jest taki, że Transformer, w przeciwieństwie do RNN, nie jest modelem sekwencyjnym. Model sekwencyjny przetwarza kolejne wyrazy, więc niejako już z tego faktu wynika, że „zna” on ich kolejność. W przypadku gdy do Transformera wrzucamy od razu całe zdanie w postacie macierzy i przetwarzamy je równolegle przez wszystkie elementy modelu, ta informacja jest tracona i musi być w jakiś sposób zastąpiona. Tę rolę pełni Positional Encoding.
e) Decoder również otrzymuje Positional Encoding (7) oraz stan tłumaczenia z momentu T-1, czyli niejako konsumuje swój output – jest to zatem model autoregresyjny. Output jest również osadzany tym samym mechanizmem, który stosujemy w encoderze (6). O tym dlaczego wejście do decodera jest oznaczone jako „Outputs – shifted right” pisałem kilka akapitów wyżej.
„Ja jestem Kowalski, a to jest pani Kowalska, innej nie chcę.” – Roch Kowalski o swej szabli
No ok, niby innej architektury niż Transformer nie chcemy, ale czy do naszego zadania na pewno potrzebna jest jej całość? Oryginalna architektura Transformer była użyta do tłumaczeń. My nie chcemy wykonać tłumaczenia, tylko wygenerować tekst. Generowaniem zajmuje się decoder a my chcemy wygenerować tekst, po tym jak uprzednio nauczyliśmy model struktury języka. Stąd, aby kontynuować wyrzucimy z naszego małego modelu cały encoder i zostaniemy tylko z decoderem. Dodatkowo, ponieważ nie mamy danych z encodera, to z decodera wypadnie również środkowy element, oznaczony na Rysunku 2 cyfrą 1, czyli multi-head attention. Architektura modelu z niniejszego tutoriala będzie ostatecznie wyglądała następująco.
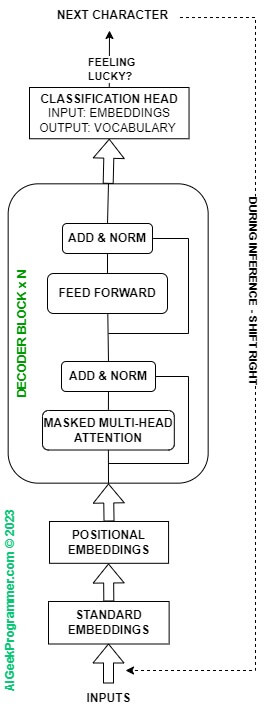
Mamy tu zatem kilka elementów do zbudowania. Zacznijmy od najprostszego, czyli „Feed Forward”. Jest to implementacja prostego multi-layer perceptron, z jedną warstwą ukrytą. Jeżeli programujesz w Pytorch, to proponuję podjąć próbę samodzielnego napisania klasy, nazwijmy ją FFNN, dziedziczącej po nn.Module, która jako parametry konstruktora przyjmie: rozmiar warstwy wejściowej (input_dim), rozmiar warstwy ukrytej (hidden_dim) i rozmiar warstwy wyjściowej (output_dim). Następnie wykona transformację liniową – nn.Linear() – z wejścia do warstwy ukrytej i z ukrytej do wyjściowej. Jako funkcję aktywacji przyjmijmy relu(), a przed zwróceniem wyniku dodajmy warstwę dropout dla regularyzacji. Oczywiście konwencja Pytorch wymaga, aby poza konstruktorem __init__(), klasa implementowała metodę forward(). Wynik swojej pracy możesz skonfrontować z kodem poniżej.
import torch
import torch.nn as nn
import torch.nn.functional as F
# class for FFNN
class FFNN(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super().__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, output_dim)
self.dropout = nn.Dropout(0.1)
def forward(self, x):
x = self.fc1(x)
x = F.relu(x)
x = self.fc2(x)
x = self.dropout(x)
return xKolejnym elementem jest masked multi-head (self) attention. Zanim jednak stworzymy klasę obsługującą ten element, przyjrzyjmy się mechanizmowi self-attention na prostym przykładzie. Mechanizm uwagi, czyli skupienia umysłu na rzeczy istotnej w danym momencie jest elementarnym procesem poznawczym u ludzi. Został on przeniesiony do domeny NLP i w ogólności do uczenia maszynowego, aby model był w stanie skupić swoją uwagę na elementach istotnie powiązanych ze sobą w zdaniu. W cytowanym już opracowaniu „Attention Is All You Need”, autorzy pokazują działanie mechanizmu uwagi w zdaniu „a majority of American governments have passed new laws since 2009 making the registration of voting process more difficult.”
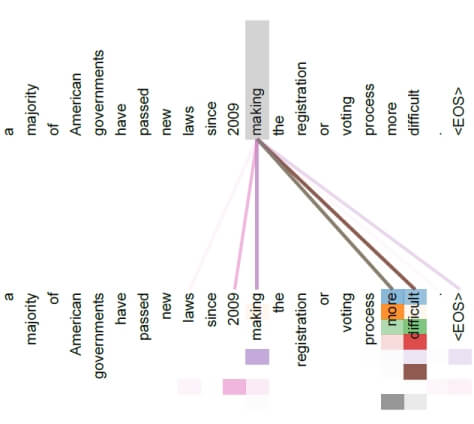
Uwaga wyliczona dla słowa making pokazuje, że mechanizm był w stanie wychwycić dość odległe, ale w oczywisty sposób istotne zależności między słowem „making” oraz „more” i „difficult”. Na rysunku intensywność koloru linii łączącej odpowiada intensywności uwagi między słowem making a pozostałymi słowami w zadaniu. Pamiętacie jeszcze Recurent Neural Networks? Ja też nie ;-). Jedną z cech RNN było to, że przetwarzają one wyrazy / tokeny sekwencyjnie, jeden za drugim. Przetwarzając kolejny wyraz w zdaniu biorą pod uwagę stan sieci dla poprzedniego tokena. W ten sposób identyfikowane są zależności między wyrazami w zdaniu. Z tym, że te zależności stawałyby się coraz słabsze wraz z oddalaniem się od słowa „making”. Część problemów RNN rozwiązało użycie LSTM i GRU, ale praktyka pokazuje, że mechanizm self-attention jest rozwiązaniem dużo efektywniejszym. Zależności między wyrazami w zdaniu mają znaczenie nie tylko dla modeli tłumaczących, ale generalnie dla wszystkich modeli językowych. Pozwalają one modelowi „zrozumieć” strukturę języka. Z tej perspektywy mechanizm self-attention staje się kluczowym elementem każdego modelu językowego.
Jak już wiemy po co mamy self-attention, to zobaczmy jak ona działa. Na wejściu, jak to w uczeniu maszynowym bywa, mechanizm otrzymuje macierz z danymi. Każdy wiersz tej macierzy jest „wyrazem”. Dla naszego przykładu przyjmijmy, że przetwarzamy jednocześnie 10 wyrazów. Innymi słowy, przyjmijmy że długość najdłuższego zdania jest równa 10 wyrazów. W praktyce te wartości są oczywiście dużo większe.
Tu mała dygresja: możliwość masowego równoległego przetwarzania wielu informacji jest główną przewagą architektury Transformer nad RNN, która jak wspominałem wyżej, przetwarza informacje sekwencyjnie a więc dużo wolniej. Innymi słowy, w architekturze Transformer wszystko odbywa się tak jak powinno, czyli na zasadzie mnożenia wielkich macierzy – a ta operacja jest bardzo lubiana przez układy GPU.
OK, zatem macierz ma 10 wierszy, każdy wiersz zawiera „wyraz” przekształcony do reprezentacji cyfrowej w procesie embeddingu (standard and positional embeddings). Przyjmijmy dla uproszczenia, że wymiar embeddingu to 32. Może być on dowolny, w oryginalnej architekturze eksperymentowano z różnymi wartościami: 128, 256, 512, pozostając ostatecznie przy tym ostatnim.
import torch
# We have input vector X of 10 tokens (rows), each token embedded in 32 dimensions (columns)
X = torch.randn(10, 32)W procesie kalkulacji uwagi definiujemy 3 macierze parametrów modelu: Query, Key i Value. Macierze te zawierają parametry modelu, czyli w procesie treningu wartości tych macierzy są uczone do wartości optymalnych:
# Query parameters matrix Q is 32x32
pQ = torch.randn(32, 32)
# Key parameters matrix K is 32x32
pK = torch.randn(32, 32)
# Value parameters matrix V is 32x32
pV = torch.randn(32, 32)Liczba wierszy tych macierzy jest taka sama jak liczba kolumn X (inaczej mnożenie się nie powiedzie). Liczba kolumn jest taka sama jak wierszy, aby zachować rozmiar wejściowy.
W pierwszym kroku mnożymy macierz wejściową X przez każdą z 3 macierzy parametrów:
# step 1 of attention: multiply parametric query matrix pQ with X
# pQ is 32x32, X is 10x32, so the result is 10x32
Q = torch.matmul(X, pQ)
# step 2 of attention: multiply parametric key matrix pK with X
# pK is 32x32, X is 10x32, so the result is 10x32
K = torch.matmul(X, pK)
# step 3 of attention: multiply parametric value matrix pV with X
# pV is 32x32, X is 10x32, so the result is 10x32
V = torch.matmul(X, pV)W rezultacie otrzymujemy trzy macierze Query, Key i Value (Q, K, V), na których wykonujemy następującą operację:
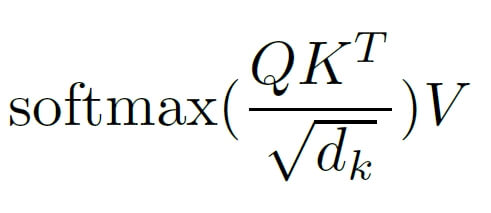
Co tu się właściwie stało? W liczniku mnożymy macierz Query przez transponowaną macierz Key. Skoro rozmiar Query to 10×32 a rozmiar transponowanej Key to 32×10 (zamieniliśmy kolumny z wierszami), to macierz wynikowa QKT będzie miała rozmiar 10×10. Co ona w zasadzie zawiera? Można ten wynik rozmieć jako odpowiedź na pytanie „Jak ważny jest klucz (key) dla zapytania (query)?”. Innymi słowy otrzymujemy wagi, które wskazują które wyrazy w analizowanym zdaniu mogą być dla siebie istotne. Oczywiście taka informacja będzie faktyczną wartościową informacją po wytrenowaniu modelu, czyli między innymi po optymalizacji wag w macierzach Query i Key.
Operacja podzielenia przez pierwiastek wymiaru klucza dk (patrz mianownik) ma za zadanie przeskalować wynik, tak aby wyeliminować potencjalnie duże wartości iloczynu macierzy. Jest to istotne, bo w dalszej kolejności wykonujemy operację softmax, która dla dużych wartości może stać się niestabilna numerycznie, czyli pojawią się bardzo duże wartości lub NaN. Po wykonaniu funkcji softmax otrzymujemy macierz 10×10, która zawiera znormalizowaną punktację wskazującą na wzajemnie istotne powiązania wyrazów w danym zdaniu. W ostatnim kroku mnożymy tę punktację przez macierz V o rozmiarze 10×32 otrzymując na wyjściu wynik self-attention o rozmiarze 10 x 32, czyli takim samym jak wejściowe X. Oto jak to może wyglądać w kodzie, na prostym przykładzie:
# step 4 of attention: calculate the attention weights
# Q is 10x32, K is 10x32, so the result is 10x10
# we need to transpose K to make it 32x10
# we need to divide by sqrt(32) to normalize the weights
weights = torch.matmul(Q, torch.transpose(K, 0, 1)) / torch.sqrt(torch.tensor(32))
# step 5 of attention: apply softmax to the weights
# weights is 10x10, so the result is 10x10
weights = torch.softmax(weights, dim=1)
# step 6 of attention: multiply the weights with the values
# weights is 10x10, V is 10x32, so the result is 10x32
output = torch.matmul(weights, V)Powyższe operacje powodują, że wraz ze stopniowym uczeniem się modelu i optymalizowaniem wartości jego parametrów pQ, pK i pV model coraz lepiej wykrywa i odwzorowuje powiązania między wyrazami w zdaniu. A powiązania te są niezbędne do wykonania tłumaczenia lub wygenerowania nowego tekstu. Na mechanizm attention można również spojrzeć przez pryzmat analogii do Convolutional Neural Networks, w których mamy operację konwolucji wykonywaną z wykorzystaniem filtrów. Filtry również są macierzami z parametrami modelu i również są uczone (optymalizowane) do tego, aby jak najlepiej wykrywały istotne cechy analizowanego obrazu.
Ociec, prać? — Prać! — odrzekł stary Kiemlicz, dobywając szablę.
To musimy jeszcze poruszyć temat masakrowania. Przepraszam, maskowania. 😉 W architekturze Transformer są dwa typy maskowania: padding oraz look-ahead. Wprawdzie paddingu w naszym rozwiązaniu nie będzie, ale i tak warto chwilę temu tematowi poświęcić. Załóżmy, że osadzamy (tzw. embedding) każdy token w przestrzeni 4 wymiarowej. Czyli każdy token przedstawimy jako wektor z 4 liczbami i że przyjęliśmy dla naszego modelu maksymalną długość zdania jako 5 tokenów. To są oczywiście wartości mało realne, ale uproszczą analizę. Teraz przyjmijmy, że w naszym zbiorze uczącym lub batchu są 2 zdania:
"Był okrutnym siepaczem" oraz "Szablą władał jak ręką"W pierwszej kolejności zamieniamy każde zdanie na tokeny. Przed wrzuceniem do modelu, chcemy aby każde zdanie miało jednakową wielkość – w naszym przykładzie 5 tokenów. Tam gdzie nam brakuje wyrazów do wielkości maksymalnej, dodajemy specjalny token <pad>. Zdania po tokenizacji wyglądają zatem następująco:
["Był", "okrutnym", "siepaczem", <pad>, <pad>] oraz ["Szablą", "władał", "jak", "ręką", <pad>]W kolejnym kroku osadzamy każdy token w postaci numerycznej, przy czym naszemu specjalnemu tokenowi <pad> przypisujemy wartość zero – poniższe wartości numeryczne są oczywiście przykładowe i wyssane z palca na potrzeby przykładu.
[[ 0.1, -0.2, 0.3, 0.5], # "Był"
[ 0.4, 0.6, -0.1, 0.2], # "okrutnym"
[ 0.7, -0.3, 0.9, -0.2], # "siepaczem"
[ 0.0, 0.0, 0.0, 0.0], # <pad>
[ 0.0, 0.0, 0.0, 0.0], # <pad>
[ 0.1, -0.2, 0.3, 0.5], # "Szablą"
[ 0.4, 0.6, -0.1, 0.2], # "władał"
[ 0.7, -0.3, 0.9, -0.2], # "jak"
[-0.5, 0.1, 0.6, -0.3], # "ręką"
[ 0.0, 0.0, 0.0, 0.0]] # <pad>Ile będzie tych paddingów w danych wejściowych? W oryginalnym artykule Vaswani et. al nie podali jednej wartości maksymalnej długości zdania, ale eksperymentowali z wartościami takimi jak 60 i 128. Może być ich zatem sporo a ich podstawowym zastosowaniem jest umożliwienie przetwarzania przez model zdań o różnej długości, z czego wywiązują się doskonale. Czy chcemy jednak aby model uczył się tych tokenów <pad>? Z oczywistych względów nie. Są one jedynie technicznym dodatkiem i model powinien je po prostu ignorować. Ignorowanie odbywa się poprzez maskowanie paddingu. Utworzenie maski może się obyć np. w taki sposób:
input_tensor = torch.tensor(
[[0.1, -0.2, 0.3, 0.5], # "Był"
[0.4, 0.6, -0.1, 0.2], # "okrutnym"
[0.7, -0.3, 0.9, -0.2], # "siepaczem"
[0.0, 0.0, 0.0, 0.0], # <pad>
[0.0, 0.0, 0.0, 0.0], # <pad>
[0.1, -0.2, 0.3, 0.5], # "Szablą"
[0.4, 0.6, -0.1, 0.2], # "władał"
[0.7, -0.3, 0.9, -0.2], # "jak"
[-0.5, 0.1, 0.6, -0.3], # "ręką"
[0.0, 0.0, 0.0, 0.0]]) # <pad>
# Please note that <pad> token is always 0.
# Create a boolean mask of the same shape as the input tensor, where True indicates a padding token
padding_mask = input_tensor.eq(0.0)
print(padding_mask)
> tensor([[False, False, False, False],
> [False, False, False, False],
> [False, False, False, False],
> [ True, True, True, True],
> [ True, True, True, True],
> [False, False, False, False],
> [False, False, False, False],
> [False, False, False, False],
> [False, False, False, False],
> [ True, True, True, True]])Nas bardziej interesuje jednak maskowanie look-ahead, które odbywa się w decoderze, przy operacji multi-head masked self-attention. Chciałbym zaznaczyć jedną ważną różnicę między padding masking a look-ahead masking. To pierwsze jest wykonywane na danej wejściowej do modelu. To drugie jest w wykonywane na macierzy wag self-attention. To jest różnica warta podkreślenia, bo może nie jest ona oczywista na pierwszy rzut oka.
Czemu maskujemy self-attention w decoderze? Chcemy wymusić na mechanizmie self-attention, aby zwracał uwagę jedynie na obecne i przeszłe tokeny, a ignorował powiązania z przyszłymi tokenami. Inaczej cały mechanizm wytrenowalibyśmy tak, aby podglądał przyszłość. W fazie treningu takie rzucenie okiem w przyszłość byłoby teoretycznie możliwe, ale w pracy wytrenowanego już modelu, to co on właściwie miałaby wtedy podglądać skoro sam tę przyszłość ma wygenerować, hę?
Maskowanie odbywa się poprzez ustawienie wag w macierzy self-attention na -inf (minus nieskończoność). Żeby było jasne: mówimy tu o macierzy będącej wynikiem operacji QKT/sqrt(dk), więc tej macierzy, którą otrzymujemy tuż przed operacją softmax. W takiej sytuacji wykonana chwilę później softmax zwróci dla wartości -inf, wartości równe 0. W ten sposób model nie będzie zwracał uwagi na wagi self-attention odpowiadające przyszłym tokenom.
Rozważmy następujący kod, w którym tworzymy najpierw tensor o wielkości 4×4 z losowymi wartościami. Następnie górną część macierzy wypełniamy zerami. Robimy to po to, aby potem wpisać w miejsca wypełnione zerami wartość -inf, która po wykonaniu operacji softmax da nam na tych pozycjach 0.
import torch
# Create a tensor with random values
t = torch.randn(4,4)
>>> tensor([[ 0.0690, 0.6172, -1.2566, -0.5793],
[-1.3215, 0.3752, 0.5788, -0.8546],
[ 0.7370, -0.2793, -0.5935, 1.1494],
[ 1.0181, -0.0314, 0.6151, -0.1329]])
# Create diagonal mask with 0s on the upper triangle
t = torch.tril(t, diagonal=0)
>>> tensor([[ 0.0690, 0.0000, 0.0000, 0.0000],
[-1.3215, 0.3752, 0.0000, 0.0000],
[ 0.7370, -0.2793, -0.5935, 0.0000],
[ 1.0181, -0.0314, 0.6151, -0.1329]])
# Fill 0s with -1e9 (minus infinity)
t = torch.masked_fill(t, t == 0, -1e9)
>>> tensor([[ 6.9021e-02, -1.0000e+09, -1.0000e+09, -1.0000e+09],
[-1.3215e+00, 3.7517e-01, -1.0000e+09, -1.0000e+09],
[ 7.3704e-01, -2.7931e-01, -5.9350e-01, -1.0000e+09],
[ 1.0181e+00, -3.1359e-02, 6.1515e-01, -1.3286e-01]])
# Apply softmax
t = torch.softmax(t, dim=1)
>>> tensor([[1.0000, 0.0000, 0.0000, 0.0000],
[0.1549, 0.8451, 0.0000, 0.0000],
[0.6149, 0.2225, 0.1625, 0.0000],
[0.4283, 0.1500, 0.2862, 0.1355]])Ktoś mógłby spytać: „Ale czemu nie wpisujemy zer w górną część macierzy po wykonaniu softmax? W ten sposób nie trzeba byłoby robić całej tej „szopki” z -inf„. Tak, ale też nie mielibyśmy sytuacji, w której wartości w każdym wierszu sumują się ostatecznie do jedności – a chcemy uzyskać stan, w którym otrzymamy rozkład prawdopodobieństwa uwagi w podziale na tokeny obecny i przeszłe, z wyłączeniem przyszłych.
„Kończ… waść! wstydu… oszczędź!” – Kmicic
Jesteśmy teraz gotowi, aby wykonać ostatni element pierwszej części tutoriala, czyli klasę realizującą masked self-attention. Dla tych, którzy chcą wykonać ten kod samodzielnie, kilka wskazówek:
- Chcemy utworzyć klasę podobną w strukturze do utworzonej wcześniej FFNN. Klasa będzie miała nazwę SingleAttentionHead i oczywiście jak to w Pytorch, musi ona dziedziczyć po nn.Module.
- W konstruktorze tworzymy 3 macierze z parametrami operacji attention o nazwach Q, K i V. Do ich implementacji sugeruję wykorzystać klasę nn.Linear, bo zapewni ona nam od razu realizację mnożenia przez macierz wejściową. W ogólności kod implementujący powinien być postaci Y = nn.Linear(input_dim, output_dim, bias=False).
- Definiując macierze Q, K i V należy podać rozmiar wejściowy i wyjściowy. Przyjmijmy, że rozmiar ten będzie definiowała globalna dla naszego skryptu zmienna o nazwie embedding_dim. Czyli będzie to zmienna zewnętrzna wobec parametrów klasy – na razie się nią nie przejmujmy.
- Zwróćcie uwagę, że nn.Linear() użyjemy tu do mnożenia macierzy, a nie do zdefiniowania warstwy sieci neuronowej, więc parametr konstruktora o nazwie bias powinien być ustawiony na False.
- Poza konstruktorem klasa dziedzicząca po nn.Module powinna również posiadać metodą forward(self, x), gdzie x będzie naszą macierzą wejściową. Nie jest to może bardzo istotne dla zdefiniowania metody forward (bo x jest jej parametrem wejściowym), ale x będzie miało rozmiar [Batch, Time, Embedding]. Pierwszy wymiar to oczywiście batch, bo dane do uczenia serwujemy w batchach. Drugi i trzeci element to właściwe dane: pozycja tokenu w zdaniu i jego embedding. O tym jak będą serwowane dane do modelu będzie w drugiej części tutoriala.
- Metoda forward(self, x) powinna w pierwszym kroku wyliczyć macierze pośrednie dla Query, Key i Value, wykorzystując zdefiniowane w konstruktorach macierze Q, K i V. Może to wyglądać tak: QX = self.Q(x)
- W kolejnym kroku należy wyliczyć wyrażenie QX*KXT/sqrt(dkx). Mnożenie macierzy można wykonać albo wykorzystując torch.matmul() jak w przykładach powyżej albo operator mnożenia macierzowego @.
- Następnie wykonujmy maskowanie i aplikujemy F.softmax(), uzyskując attention.
- Ostatnim krokiem jest przemnożenie attention przez macierz VX i zwrócenie tej macierzy jako wynik działania metody forward().
Proste, nie? Żartuję, lol.
Tylko pamiętajcie: jak chcecie programować samodzielnie, to nie można za szybko patrzeć na gotowe rozwiązanie. Tego się chyba wszyscy nauczyliśmy grając w kurę, prawda? XD

Gotowy kod klasy SingleAttentionHead:
import torch
import torch.nn as nn
import torch.nn.functional as F
# class for a single Head of Attention (SingleAttentionHead)
class SingleAttentionHead(nn.Module):
def __init__(self):
super().__init__()
self.Q = nn.Linear(embedding_dim, embedding_dim, bias=False)
self.K = nn.Linear(embedding_dim, embedding_dim, bias=False)
self.V = nn.Linear(embedding_dim, embedding_dim, bias=False)
def forward(self, x):
# x is [Batch, Time, Embedding]
QX = self.Q(x)
KX = self.K(x)
VX = self.V(x)
# calculate score
score = QX @ torch.transpose(KX, 1, 2) / torch.sqrt(torch.tensor(embedding_dim, dtype=torch.float32))
# mask the score
mask = torch.tril(torch.ones(score.shape, device=device), diagonal=0)
score = score.masked_fill(mask == 0, float('-inf'))
# softmax over the last dimension
attention = F.softmax(score, dim=-1)
# multiply the attention with the value
out = attention @ VX
return outNa tym zakończę pierwszą część tutoriala. Mam wrażenie, że wyszedł z tego spory materiał, który teraz może się wydawać nieco nieuporządkowany, bo poruszyliśmy wiele tematów. Warto jednak te informacje przetrawić, bo będą się one powoli układały w bardziej spójną całość w kolejnej części.
____________________________________
Przypisy:
1) Attention is All You need
2) Andrej Karpathy „Neural networks: Zero to Hero” video tutorial
