k najbliższych sąsiadów w klasyfikacji pisma

W uczeniu maszynowym jest takie stare, ale sprawdzone powiedzenie: „Nie da ci ojciec, nie da ci matka, tego co może dać ci … k najbliższych sąsiadów”. 😉 Nie wierzycie? Ja też nie mogłem w to uwierzyć, póki nie spróbowałem sklasyfikować pisma odręcznego z użyciem tego algorytmu. k najbliższych sąsiadów – z ang. k-nearest neighbours lub po prostu KNN – nie jest może pierwszą myślą, jaka przychodzi do głowy przy klasyfikacji pisma, ale jak się okazuje, użycie tej metody wcale nie jest pozbawione sensu.

Z niniejszego posta dowiesz się między innymi:

• Jakie są najważniejsze cechy KNN i w jakich klasach zagadnień można jej użyć?
• Na jakiej zasadzie działa metoda k najbliższych sąsiadów?
• Jak można skutecznie sklasyfikować pismo odręczne z wykorzystaniem KNN?
  

Co na pewno trzeba wiedzieć o k najbliższych sąsiadów?

KNN jest bardzo prostym do zrozumienia i zaimplementowania algorytmem. Jednocześnie oferuje on zaskakująco wysoką skuteczność w zastosowaniach praktycznych. Jego prostota, która z całą pewnością bywa jego zaletą, jest jednocześnie cechą, która sprawia, że czasami niepotrzebnie pomija się go przy rozwiązywaniu bardziej skomplikowanych problemów. Co ciekawe, zastosowanie algorytmu jest bardzo szerokie. Możemy przeprowadzić z jego użyciem zarówno uczenie nienadzorowane, jak i nadzorowane: w zakresie regresji oraz klasyfikacji. I tym ostatnim zajmiemy się w niniejszym poście, w dalszej jego części, próbując sklasyfikować pismo odręczne.

Czytając formalne definicje, można zauważyć, że KNN jest charakteryzowany jako algorytm nieparametryczny i „leniwy” (non-parametristic and lazy). Nieparametryczny w tym przypadku nie oznacza wcale, że nie mamy tu żadnych hiperparametrów – bo przecież choćby mamy najważniejszy parametr, jakim jest liczba k, czyli liczba sąsiadów. Oznacza to tylko tyle, albo aż tyle, że algorytm ten nie zakłada z góry, iż mamy do czynienia z pewnym rozkładem danych. Jest to bardzo przydatne założenie, bo w świecie rzeczywistym dane, którymi dysponujemy, często nie są łatwo separowalne liniowo lub niezbyt dobrze odwzorowują dystrybucję normalną czy jakąkolwiek inną. Stąd KNN może się przydawać, szczególnie w przypadkach, gdy zależność między danymi wejściowymi a wynikiem jest nietypowa lub bardzo złożona, co sprawia, że klasyczne metody w rodzaju regresji liniowej lub logistycznej mogą nie podołać zadaniu.

„Leniwy” z kolei oznacza, że algorytm nie buduje modelu generalizującego dany problem w fazie uczenia. Można powiedzieć, że uczenie jest odroczone do momentu, kiedy do modelu trafia zapytanie. Z powyższego faktu płyną dwa istotne dla KNN wnioski. Po pierwsze, faza testowania lub predykcji będzie trwała dłużej niż faza „uczenia się”. Po drugie, w większości przypadków KNN będzie potrzebował w trakcie predykcji mieć dostępne wszystkie dane ze zbioru uczącego – to z kolei, przy dużych zbiorach, nakłada dość spore wymagania na ilość pamięci.

Jak to działa – prosty przykład

Działanie algorytmu najlepiej wyjaśnić graficznie i w przestrzeni dwuwymiarowej. Załóżmy, że mamy zbiór danych opisany dwoma cechami (tu reprezentowanymi przez współrzędne na płaszczyźnie) i sklasyfikowany na dwie klasy: koła i trójkąty.

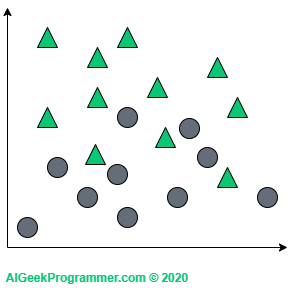
Jak widać, ten zbiór jest dość łatwo separowalny liniowo, więc pewnie wystarczyłoby np. wykorzystać regresję logistyczną dla klasyfikacji binarnej, aby uzyskać świetny efekt, ale dla celów wytłumaczenia zasady działania algorytmu, taki przykład nada się doskonale.

Załóżmy teraz, że mając taki zbiór, chcemy sklasyfikować nowy obiekt (czerwona plama) jako trójkąt lub koło:

KNN działa w ten sposób, że patrzy na „najbliższą okolicę” nowej danej i sprawdza, jakiej klasy obiektów jest tam więcej i na podstawie tego decyduje o opisaniu jej albo jako trójkąt, albo jako koło. Okay, ale co rozumiemy poprzez „najbliższą okolicę”? I tu do gry wchodzi parametr k, który określa na ilu najbliższych sąsiadów chcemy spojrzeć. Jeżeli spojrzymy na jednego (co jest raczej rzadko spotykaną wartością parametru k), to okaże się, że nasza nowa dana jest trójkątem.

Jeżeli pod uwagę weźmiemy trzech sąsiadów, to nasza czerwona próbka zmieni się w koło – zupełnie jak w fizyce kwantowej: 😉

Z kolei dla k=5 znowu mamy do czynienia z klasyfikacją jako trójkąt, bo w najbliższym otoczeniu są trzy trójkąty i dwa koła:

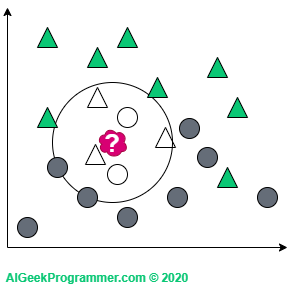
Warto tu zauważyć dwie kwestie. Jak widać, wartości k przyjąłem nieparzyste. Jest to o tyle uzasadnione, że nie trafimy na przypadek, w którym nowa dana jest w sąsiedztwie dwóch kół i dwóch trójkątów. Nie oznacza to, że takich wartości k nie stosuje się w praktyce. Po prostu dla powyższego przykładu niepotrzebnie skomplikowałoby to tok naszego rozumowania. Po drugie, nowa dana pojawiła się niejako na granicy dwóch klas. Stąd raz jest ona kołem, a raz trójkątem, w zależności od wartości parametru k. Jeżeli jednak nowy obiekt pojawi się w innym, bardziej „trójkątnym” miejscu, to bez względu na wartość parametru k, pozostanie on trójkątem:

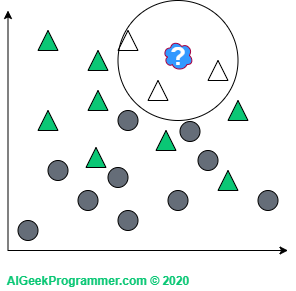
k najbliższych sąsiadów – nieco głębsze spojrzenie

Mimo, że KNN jest niezwykle prosty, to jednak jest kilka zagadnień, które warto nieco zgłębić, bo jak zwykle diabeł tkwi w szczegółach.

W jaki sposób liczymy odległość?

Wydaje się to dość oczywiste, ale warto w tym miejscu podkreślić, że warunkiem koniecznym do zastosowania algorytmu k najbliższych sąsiadów na danym zbiorze jest możliwość wyliczenia odległości między elementami tego zbioru. Nie musi być to odległość euklidesowa, ale brak możliwości kalkulacji odległości w zasadzie eliminuje KNN z analizy takiego zbioru danych.

W dwuwymiarowej przestrzeni euklidesowej, którą rozważaliśmy powyżej, odległość może być wyliczona z twierdzenia Pitagorasa. Ponieważ jednak rzadko kiedy analizujemy zbiór danych tylko z dwoma cechami (dwuwymiarowy), to uogólniając problem odległości do przestrzeni n wymiarowej, funkcję odległości można zdefiniować następującą metryką:

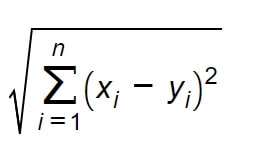
Jest to najczęstszy sposób wyliczenia odległości, ale nie jedyny. Biblioteka scikit-learn, której użyjemy w tym poście nieco później, oferuje możliwość użycia kilkunastu różnych metryk, w zależności od rodzaju danych i typu zadania.

Jak dobrać wartość k?

Liczba k jest hiperparametrem i tak jak w przypadku innych hiperparametrów w uczeniu maszynowym, nie ma reguły ani wzoru na ustalenie jej wartości. Najlepiej zatem ustalić ją eksperymentalnie, oceniając skuteczność predykcji dla różnych wartości k. Dla dużych zbiorów może to być jednak czasochłonne. Przyda się kilka wskazówek:

• W dość oczywisty sposób małe wartości k będą niosły ze sobą większe ryzyko niepoprawnej klasyfikacji.
• Z kolei duże wartości k dadzą pewniejsze wyniki, ale będą dużo bardziej wymagające obliczeniowo. Poza tym wartość k ustawiona dajmy na to na 80, intuicyjnie kłóci się ideą najbliższych sąsiadów. W końcu chodzi o to, aby spojrzeć na najbliższe otoczenie nowego punktu danych.
• W klasyfikacji binarnej dobrze jest używać wartości nieparzystych, aby uniknąć konieczności dokonywania losowego wyboru w przypadku równego podziału głosów.
• Jedną z polecanych dość powszechnie wartości k do wypróbowania jest pierwiastek kwadratowy z ilości elementów w zbiorze uczącym. Dla przykładu, jeżeli nasz zbiór uczący ma 1000 elementów, to jako jedną z wartości k powinniśmy rozważyć 32. Dla 50 000 będzie to już 224. Osobiście nie jestem przekonany do tej metody. Nie znalazłem również jej pochodzenia ani naukowego wytłumaczenia (co nie oznacza, że ono nie istnieje). Uważam, że uzyskiwane w ten sposób wartości są za wysokie.
• Metodą, którą dla mnie wydaje się rozsądniejsza jest pierwiastek 4 stopnia z ilości danych w zbiorze uczącym. Dla 500 próbek k będzie wynosić 5, dla 1000 k=6, dla 50 000 jest to 15, a wartości powyżej 30 stosujemy dla zbiorów o ilości danych przekraczających milion.
• Są również metody, które głosują nie na podstawie wybrania ze zbioru k najbliższych sąsiadów, ale na podstawie głosów zebranych z danych znajdujących się w określonym promieniu od badanego punktu. Taki klasyfikator – Radius Neighbors Classifier – oferuje między innymi biblioteka scikit-learn.
• Trzeba jednak wyraźnie zaznaczyć, że ustalenie optymalnej wartości k jest mocno zależne od danych i rozważanego problemu, stąd do powyższych wskazówek i wzorów trzeba podchodzić krytycznie i przede wszystkim samemu szukać najlepszego rozwiązania.

Co jeżeli liczba sąsiadów jest taka sama w dwóch lub więcej klasach?

Jest to ciekawy przypadek, gdyż w takiej sytuacji jest tak samo prawdopodobne, że badana próbka należy do jednej z tych dwóch lub więcej klas. Rozwiązaniem może być wybór losowy lub przypisanie wagi dla każdego z k najbliższych sąsiadów. Czym sąsiad bliższy, tym jego waga bardziej istotna. Biblioteka scikit-learn oferuje specjalny parametr „weights”, który ustawiony na wartość 'uniform’ zakłada, że każdy sąsiad ma taką samą wagę, a ustawiony na wartość 'distance’ przypisuje sąsiadom wagę odwrotnie proporcjonalną do jego odległości od badanego punktu danych.

A co z efektywnością obliczeń?

Wraz ze wzrostem ilości danych (N) w zbiorze uczącym, istoty nabiera kwestia efektywności obliczeń. Najmniej wyrafinowanym podejściem jest zastosowanie 'brute force’, czyli wyliczenie odległości między badanym punktem, a wszystkimi punktami zbioru uczącego. Koszt takiej metody rośnie wykładniczo, wraz ze wzrostem N. Dla zbiorów rzędu kilkunastu tysięcy próbek i większych stosowanie 'brute force’ jest w zasadzie niepraktyczne lub nieuzasadnione. Stąd stosuje się często bardziej wyrafinowane metody, oparte o struktury drzewiaste, które sprowadzają się do selekcji punktów leżących blisko badanego punktu danych. W uproszczeniu: jeżeli punkt X leży bardzo daleko od punktu Y, a punkt Z leży bardzo blisko punktu Y, to można założyć, że punkty X i Z leżą daleko od siebie i nie ma potrzeby wyliczania dla nich dystansu. Scikit-learn implementuje dwie takie struktury: K-D Tree oraz Ball Tree. O ich zastosowaniu biblioteka decyduje sama, na podstawie charakterystyki zbioru danych, chyba że celowo narzucimy jej użycie jednego z trzech ww. sposobów. Szczegółowo jest to opisane w tej sekcji.

k najbliższych sąsiadów w klasyfikacji pisma odręcznego

Okay, po solidnej dawce teorii sprawdźmy, jak KNN poradzi sobie z zagadnieniem praktycznym. Biblioteka scikit-learn udostępnia rozbudowane narzędzia dla algorytmu k najbliższych sąsiadów –  szkoda byłoby nie skorzystać. Na rozgrzewkę na warsztat weźmiemy jeden z testowych zbiorów udostępnianych przez scikit-learn – The Digits Dataset.

Dla celów poniższego zadania najlepiej utworzyć nowe środowisko wirtualne condy. Jeżeli chcesz się dowiedzieć więcej o środowiskach wirtualnych, zapraszam do zapoznania się z tym postem. Na Windows wystarczy uruchomić Anaconda prompt, przejść do katalogu, w którym chcemy zapisywać skrypty i wykonać trzy komendy:

conda create --name <nazwa>
conda activate <nazwa>
conda install numpy matplotlib scikit-learn jupyter keras

Z tak skonfigurowanego środowiska można skorzystać, uruchamiając jupyter notebook lub konfigurując projekt bazujący na tym środowisku w Waszym ulubionym IDE.

Wykonując klasyfikację, będziemy musieli skorzystać z szeregu komponentów, które na początku należy zaimportować. Jest to też dobry test na to, czy środowisko zostało poprawnie utworzone i aktywowane:

from sklearn import datasets, neighbors
from sklearn.model_selection import train_test_split
from keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np
from random import randint
import time

W pierwszym kroku zaimportowaliśmy testowe zbiory danych, w tym Digits, a także klasyfikator knn. W dalszej części posta potrzebna nam będzie również funkcja dzieląca zbiór danych na uczący i testowy oraz bardziej zaawansowany zbiór MNIST, który pobierzemy z biblioteki Keras. Wyświetlanie wyników w formie graficznej zapewni nam matplotlib, a do części operacji na zbiorze danych wykorzystamy oczywiście numpy. Na sam koniec dwa importy funkcji narzędziowych, związanych z generowaniem liczb losowych i pomiarem czasu.

Jeżeli wszystkie importy wykonały się prawidłowo, możemy przystąpić do dalszego kodowania. Do pobrania zbioru danych Digits użyjemy funkcji narzędziowych oferowanych przez scikit-learn:

# load Digits data set divided into data X and labels y
X, y = datasets.load_digits(return_X_y=True)

# check data shapes - data is already flattened
print("X shape:", X.shape[0:])
print("y shape:", y.shape[0:])
>>> X shape: (1797, 64)
>>> y shape: (1797,)

Metoda load_digits, odpowiednio sparametryzowana, zwróciła nam dane do zmiennej X, a etykiety do zmiennej y. Zobaczmy kilkanaście losowo wybranych elementów zbioru Digits:

# let's see some random data samples.
pics_count = 16
digits = np.zeros((pics_count,8,8), dtype=int)
labels = np.zeros((pics_count,1), dtype=int)
for i in range(pics_count):
    idx = randint(0, X.shape[0]-1)
    # as data is flattened we need them to be reshaped to the original 2D shape
    digits[i] = X[idx].reshape(8,8)
    labels[i] = y[idx]

# then we print them all
fig = plt.figure()
fig.suptitle("A sample from the original dataset", fontsize=18)
for n, (digit, label) in enumerate(zip(digits, labels)):
    a = fig.add_subplot(4, 4, n + 1)
    plt.imshow(digit)
    a.set_title(label[0])
    a.axis('off')
fig.set_size_inches(fig.get_size_inches() * pics_count / 7)
plt.show()

Nie ma się co oszukiwać, nie wygląda to jak grafika w World of Tanks, ale większość kształtów jest dość prosta do sklasyfikowania ludzkim okiem. Swoją drogą ciekawe, jak dużo cyfr bylibyśmy w stanie samemu szybko sklasyfikować i czy ta klasyfikacja byłaby lepsza od wyniku algorytmu. 😉

Dzielimy zbiór na uczący (70% danych) i testowy (30% danych), aby zasymulować sytuację, w której otrzymujemy nowe dane – tymi nowymi danymi będzie zbiór testowy – a następnie klasyfikujemy je na podstawie zbioru uczącego. Pamiętajmy, że w przypadku KNN nie mamy klasycznego uczenia, bo klasyfikator jest „leniwy”:

# splitting into train and test data sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

Sprawdźmy kształty uzyskanych w ten sposób zmiennych:

# checking shapes
print("X train shape:", X_train.shape[0:])
print("y train shape:", y_train.shape[0:])
print("X test shape:", X_test.shape[0:])
print("y test shape:", y_test.shape[0:])
>>> X train shape: (1257, 64)
>>> y train shape: (1257,)
>>> X test shape: (540, 64)
>>> y test shape: (540,)

Mając dane załadowane do zmiennych, zdefiniujemy sobie funkcję klasyfikującą (lets_knn), którą potem wykorzystamy również przy innym zbiorze. Funkcja przyjmuje na wejściu oba zbiory oraz ich etykiety, tworzy klasyfikator, przetwarza zbiór uczący (knn.fit), a następnie przeprowadza predykcję i określa jakość klasyfikacji (accuracy). Na sam koniec wyświetlamy wyniki klasyfikacji, a także identyfikujemy, które dane zostały sklasyfikowane nieprawidłowo (wrong_pred), jaką otrzymały etykietę (wrong_labels), a jaką powinny (correct_labels).  Funkcja akceptuje również, jako parametry, liczbę sąsiadów, sposób określania wag dla odległości oraz parametr określający, czy prezentować w formie graficznej błędne predykcje:

def lets_knn(X_train, y_train, X_test, y_test, n_neighbors=3, weights='uniform', print_wrong_pred=False):
    t0 = time.time()
    # creating and training knn classifier
    knn = neighbors.KNeighborsClassifier(n_neighbors=n_neighbors, weights=weights)
    knn.fit(X_train, y_train)
    t1 = time.time()

    # predicting classes and comparing them with actual labels
    pred = knn.predict(X_test)
    t2 = time.time()
    # calculating accuracy
    accuracy = round(np.mean(pred == y_test)*100, 1)

    print("Accuracy of", weights ,"KNN with", n_neighbors, "neighbors:", accuracy,"%. Fit in",
          round(t1 - t0, 1), "s. Prediction in", round(t2 - t1, 1), "s")

    # selecting wrong predictions with correct and wrong labels
    wrong_pred = X_test[(pred != y_test)]
    correct_labels = y_test[(pred != y_test)]
    wrong_labels = pred[(pred != y_test)]

    if print_wrong_pred:
        # the we print first 16 of them
        fig = plt.figure()
        fig.suptitle("Incorrect predictions", fontsize=18)
        # in order to print different sized photos, we need to determine to what shape we want to reshape
        size = int(np.sqrt(X_train.shape[1]))
        for n, (digit, wrong_label, correct_label) in enumerate(zip(wrong_pred, wrong_labels, correct_labels)):
            a = fig.add_subplot(4, 4, n + 1)
            plt.imshow(digit.reshape(size,size))
            a.set_title("Correct: " + str(correct_label) + ". Predicted: " + str(wrong_label))
            a.axis('off')
            if n == 15:
                break
        fig.set_size_inches(fig.get_size_inches() * pics_count / 7)
        plt.show()

Wykorzystajmy powyższą funkcję do wykonania predykcji dla zbioru Digits:

lets_knn(X_train, y_train, X_test, y_test, 5, 'uniform', print_wrong_pred=True)
>>> Accuracy of uniform KNN with 5 neighbors: 98.0 %. Fit in 0.0 s. Prediction in 0.1 s

Funkcja została wywołana dla k=5 sąsiadów, z jednolitymi wagami (’uniform’) dla każdej odległości i uzyskała przyzwoitą poprawność na poziomie 98%.

Spójrzmy, które z danych zostały sklasyfikowane niepoprawnie:

No, nie wiem, 🙂 dyskutowałbym z „poprawnymi” opisami niektórych labelek lub przynajmniej musiałbym nieco dłużej zastanowić się nad prawidłową odpowiedzią. Jak widać, KNN dał radę, bo powyższe to wszystkie błędne predykcje na 540 próbek testowych.

Sprawdźmy teraz, jak nasz klasyfikator poradzi sobie z dużo większym i bardziej wymagającym zbiorem danych, jakim jest MNIST. Gdyby ktoś chciał się dowiedzieć nieco więcej o zbiorze MNIST, to pisałem o nim na samym początku postu nt. klasyfikacji pisma odręcznego. Zbiór MNIST jest prosty do załadowanie przy wykorzystaniu loadera z biblioteki Keras:

# now let's play with MNIST data set
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# checking initial shapes
print("X train initial shape:", X_train.shape[0:])
print("y train initial shape:", y_train.shape[0:])
print("X test initial shape:", X_test.shape[0:])
print("y test initial shape:", y_test.shape[0:])
>>> X train initial shape: (60000, 28, 28)
>>> y train initial shape: (60000,)
>>> X test initial shape: (10000, 28, 28)
>>> y test initial shape: (10000,)

Jak widać, mamy do dyspozycji 60 000 próbek w zbiorze uczącym i 10 000 w zbiorze testowym. Dodatkowo każdy element ze zbioru, to obrazek o wymiarach 28 x 28, co w porównaniu do zbioru Digits, z jego 8 x 8, daje ponad 12-krotnie większy wymiar danych. Klasyfikacja na takiej ilości danych zabierze sporo czasu. Zgodnie z tym, co rozważaliśmy powyżej, KNN jest klasyfikatorem leniwym, co oznacza, że większość obliczeń następuje w fazie predykcji. Warto więc ograniczyć ilość danych w zbiorze testowym, co znacząco powinno przyspieszyć uzyskanie wyników. Oczywiście, jeżeli dysponujecie odpowiednio mocnym środowiskiem obliczeniowym lub macie dużo czasu, możecie eksperymentować z wartościami większymi. Niestety, biblioteka scikit-learn nie oferuje wsparcia dla GPU:

# Reducing the size of testing data set, as it's the most time-consuming
X_train = X_train[:60000]
y_train = y_train[:60000]
X_test = X_test[:1000]
y_test = y_test[:1000]

Dane pobrane loaderem są dwuwymiarowe: 28 x 28. Uczenie maszynowe oczekuje płaskiego wektora, stąd musimy je spłaszczyć:

# reshaping
X_train = X_train.reshape((-1, 28*28))
X_test = X_test.reshape((-1, 28*28))

# checking shapes
print("X train shape:", X_train.shape[0:])
print("y train shape:", y_train.shape[0:])
print("X test shape:", X_test.shape[0:])
print("y test shape:", y_test.shape[0:])
>>> X train shape: (60000, 784)
>>> y train shape: (60000,)
>>> X test shape: (1000, 784)
>>> y test shape: (1000,)

Jesteśmy obecnie gotowi do uruchomienia naszego klasyfikatora. Aby było ciekawiej, uruchomimy go dla różnych wartości k oraz dla dwóch sposobów określania wag najbliższych sąsiadów:

# lets run it with different parameters to check which one is the best
for weights in ['uniform', 'distance']:
    for n in range(1,11):
        lets_knn(X_train, y_train, X_test, y_test, n_neighbors=n, weights=weights, print_wrong_pred=True)

>>> Accuracy of uniform KNN with 1 neighbors: 96.2 %. Fit in 49.2 s. Prediction in 63.5 s
>>> Accuracy of uniform KNN with 2 neighbors: 94.8 %. Fit in 50.4 s. Prediction in 61.4 s
>>> Accuracy of uniform KNN with 3 neighbors: 96.2 %. Fit in 47.6 s. Prediction in 61.4 s
>>> Accuracy of uniform KNN with 4 neighbors: 96.4 %. Fit in 46.1 s. Prediction in 61.0 s
>>> Accuracy of uniform KNN with 5 neighbors: 96.1 %. Fit in 47.2 s. Prediction in 60.7 s
>>> Accuracy of uniform KNN with 6 neighbors: 95.9 %. Fit in 46.1 s. Prediction in 60.7 s
>>> Accuracy of uniform KNN with 7 neighbors: 96.2 %. Fit in 46.4 s. Prediction in 60.8 s
>>> Accuracy of uniform KNN with 8 neighbors: 95.8 %. Fit in 47.5 s. Prediction in 60.8 s
>>> Accuracy of uniform KNN with 9 neighbors: 95.2 %. Fit in 46.3 s. Prediction in 61.8 s
>>> Accuracy of uniform KNN with 10 neighbors: 95.4 %. Fit in 50.8 s. Prediction in 62.8 s
>>> Accuracy of distance KNN with 1 neighbors: 96.2 %. Fit in 48.7 s. Prediction in 63.1 s
>>> Accuracy of distance KNN with 2 neighbors: 96.2 %. Fit in 53.2 s. Prediction in 63.5 s
>>> Accuracy of distance KNN with 3 neighbors: 96.5 %. Fit in 51.5 s. Prediction in 63.0 s
>>> Accuracy of distance KNN with 4 neighbors: 96.4 %. Fit in 50.3 s. Prediction in 60.5 s
>>> Accuracy of distance KNN with 5 neighbors: 96.4 %. Fit in 46.0 s. Prediction in 60.4 s
>>> Accuracy of distance KNN with 6 neighbors: 96.5 %. Fit in 48.5 s. Prediction in 61.5 s
>>> Accuracy of distance KNN with 7 neighbors: 96.4 %. Fit in 48.6 s. Prediction in 61.5 s
>>> Accuracy of distance KNN with 8 neighbors: 96.4 %. Fit in 48.3 s. Prediction in 61.5 s
>>> Accuracy of distance KNN with 9 neighbors: 95.7 %. Fit in 48.1 s. Prediction in 61.6 s
>>> Accuracy of distance KNN with 10 neighbors: 95.7 %. Fit in 48.4 s. Prediction in 61.5 s

Wyniki są bardzo zbliżone dla wszystkich konfiguracji. Nie wklejałem wyników dla większych k, ale podnoszenie wartości parametru, nawet do 20, nie zmienia sytuacji. Wydaje się, że dla zbioru MNIST nieco lepsze efekty daje ważone mierzenie odległości – 'distance’ – dla którego zarejestrowaliśmy dwa najlepsze wyniki klasyfikacji 96,5% dla k=3 i tyle samo dla k=6. Warto również zwrócić uwagę na dużo większe czasy wykonania klasyfikacji niż w przypadku zbioru Digits – około 49 s trwa faza „uczenia”, a około 61 s faza predykcji.

Na sam koniec rzućmy jeszcze okiem na przykłady błędnej klasyfikacji:

Za wyjątkiem kilku pozycji: (wiersz 1, kolumna 3), (2,1), (3,3), (4,3) i (4,4), błędy są nieco bardziej oczywiste niż w przypadku zbioru Digits. Niemniej, klasyfikacja na poziomie 96,5% dla tak prostego w założeniach algorytmu może robić dobre wrażenie.

W niniejszym poście przybliżyłem Wam teoretyczne podstawy stojące za metodą k najbliższych sąsiadów. Zastosowaliśmy również algorytm w praktyce, rozwiązując dwa problemy klasyfikacyjne. KNN, mimo swojej prostoty i niewątpliwej łatwości użycia, daje bardzo dobre wyniki w szeregu zagadnień i mam nadzieję, że zachęciłem Was do częstszego korzystania z tej metody.

---

Masz pytanie? Zadaj je w komentarzu.

Spodobał ci się post? Będzie mi miło, gdy go polecisz.

Do zobaczenia wkrótce, przy okazji omawiania innego ciekawego tematu!