Konwolucyjne sieci neuronowe 3: overfitting

Konwolucyjne sieci neuronowe to jedna z najbardziej skutecznych architektur sieci neuronowych w obszarze klasyfikacji obrazów. W pierwszej części tutoriala omówiliśmy zagadnienie konwolucji oraz zbudowaliśmy prostą, gęsto połączoną sieć neuronową, której użyliśmy do klasyfikacji zbioru CIFAR-10, uzyskując skuteczność na poziomie 47%. W części drugiej tutoriala zapoznaliśmy się szczegółowo z architekturą i parametrami konwolucyjnej sieci neuronowej, zbudowaliśmy własną sieć i uzyskaliśmy na niej ~70% skuteczność klasyfikacji na zbiorze testowym. Jak się okazało, zetknęliśmy się jednak z problemem overfittingu, który uniemożliwił nam uzyskanie lepszych rezultatów. W tej części tutoriala przyjrzymy się bliżej kwestii overfittingu oraz poznamy różne techniki regularyzacji, czyli przeciwdziałania nadmiernemu dopasowaniu do zbioru uczącego. Post zakończymy listą praktycznych wskazówek, które mogą być przydatne przy okazji budowy konwolucyjnej sieci neuronowej.

Z trzeciej części tutoriala dowiesz się:

• Czym jest overfitting?
• Jak poradzić sobie z problemem overfittingu?
• Co to jest internal covariate shift?
• Jak zastosować normalizację batchową?
• Na czym polega dropout?
• Poznasz też kilka praktycznych porad dotyczących budowania konwolucyjnych sieci neuronowych.

---

Czy oglądasz mecze NBA? Sprawdź mój darmowy serwis NBA Games Ranked i ciesz się oglądaniem wyłącznie dobrych meczów.

---

Czym jest overfitting?

Sięgnijmy raz jeszcze do wyników uczenia naszej sieci konwolucyjnej z części drugiej tutoriala. Na Rysunku 1 widać wynik klasyfikacji na zbiorze treningowym, który ostatecznie sięgnął nawet 95% (linia niebieska). Pod nim wyrysowany jest wynik klasyfikacji na zbiorze walidacyjnym (linia pomarańczowa). Jak widać, wyniki dla obu zbiorów zaczęły się oddalać od siebie już w okolicy 15 epoki, a ostateczna różnica dla 80 epoki wyniosła nawet ~25%.

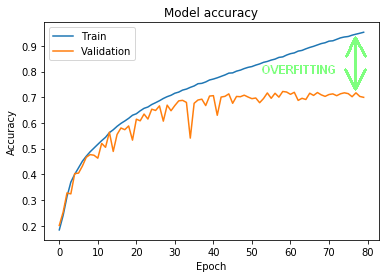
Taką sytuację nazywamy overfittingiem. Sieć na tyle dobrze nauczyła się klasyfikować zbiór treningowy, że utraciła jednocześnie zdolność do generalizowania, czyli umiejętność poprawnej klasyfikacji danych, których uprzednio nie widziała.

Aby lepiej zrozumieć overfitting, wyobraźmy sobie przykład z życia wzięty. Zawodowy koszykarz musi mieć buty najwyższej jakości. Współpracuje z firmą produkującą obuwie, a firma ta przygotowuje buty, które są idealnie dopasowane do kształtu i budowy jego stopy. Z reguły wymaga to nie tyle dopasowania kształtu buta, ile wykonania specjalnie dobranej wkładki. Koszykarz świetnie czuje się w nowych butach i jego gra jest jeszcze lepsza. Czy to oznacza, że tak wykonane buty będą równie dobre dla innego koszykarza lub dla graczy-amatorów? Prawdopodobnie w zdecydowanej większości przypadków nie. Te buty zostały na tyle dokładnie dopasowane do stopy tego konkretnego koszykarza, że nie będą się dobrze sprawowały na innej stopie. Jest to overfitting, a firmy produkujące obuwie dla szerokiego grona klientów starają się je zaprojektować w taki sposób, aby kształty buta i wkładki pasowały na jak największą liczbę stóp, zapewniając jednocześnie jak największy komfort gry.

Jeszcze inny przykład – tym razem graficzny. Załóżmy, że chcemy zbudować klasyfikator, który będzie poprawnie klasyfikował dane na „koliste” i „trójkątne”.

Jeżeli zbyt mocno dopasujemy klasyfikator do danych uczących, to nie będzie on w stanie poprawnie klasyfikować nowych danych, bo jest raczej mało prawdopodobne, aby te nowe dane wpasowywały się idealnie w rozkład danych treningowych. Stąd lepiej, aby model był nieco mniej skomplikowany / mniej złożony. Będzie wprawdzie osiągał nieco gorsze wyniki na zbiorze uczącym, ale za to zdecydowanie lepiej będzie generalizował problem, czyli również poprawniej klasyfikował nowe dane.

Jak rozwiązać problem overfittingu?

Ok, w takim razie w jaki sposób przeciwdziałać overfittingowi? Jest na to co najmniej kilka skutecznych metod. Poniżej opiszę najważniejsze i postaramy się zastosować część z nich w naszym klasyfikatorze.

Zbieramy więcej danych – jest to często najbardziej skuteczna metoda, aby zapobiec nadmiernemu dopasowaniu. Jeżeli model zobaczy więcej danych, będzie w stanie lepiej generalizować swoją odpowiedź. Pamiętajmy, że sieci neuronowe, czy też – uogólniając – uczenie maszynowe uwielbia ogromne ilości danych i duże moce obliczeniowe. Niestety, często metoda ta jest najtrudniejsza do zastosowania w praktyce lub wręcz niemożliwa – jak w naszym przypadku, gdy mamy zamknięty zbiór danych.

Jeżeli nie możemy zebrać większej ilości danych, to czasami możemy je samodzielnie wytworzyć. Jakkolwiek brzmi to dość karkołomnie i może zastanawiać założenie, że sztucznie wytworzone dane poprawią odpowiedź modelu, ale w praktyce metoda ta przynosi dobre efekty. Szczególnie w przetwarzaniu obrazu mamy szerokie pole do popisu. Możemy obrazek lekko obrócić, przesunąć, zmienić jego kolory lub dokonać innych mniej lub bardziej subtelnych zmian, które dadzą modelowi tony nowych danych. Z logicznego punktu widzenia: dysponując oryginalnym zdjęciem konia, możemy dokonać jego lustrzanego odbicia lub zmiany barwy i nadal będzie to zdjęcie konia. Technika ta nosi nazwę data augmentation i czołowe biblioteki oferują gotowe narzędzia do wykorzystania. Z jednego z nich skorzystamy w następnej części  tutoriala.

Jak już wspominałem w drugiej części tutoriala, każda sieć neuronowa posiada wiele tzw. hiperparametrów. Mają one istotny wpływ na sposób działania sieci. Stanowią część architektury modelu i sterując nimi, można uzyskiwać lepsze lub gorsze wyniki. Przy budowie każdego modelu warto eksperymentalnie poszukać architektury, która daje nam lepsze rezultaty. Czasami zmniejszenie złożoności architektury daje zaskakująco dobre efekty. Zbyt złożona architektura będzie w stanie dość szybko wygenerować overfitting, bo będzie jej łatwiej dokładnie dopasować się do zbioru uczącego.

Zaczniemy właśnie od tego prostego ruchu. Sieć z części drugiej tutoriala składa się z podsieci konwolucyjnej i gęsto połączonej. Sieć konwolucyjna nie jest gęsto połączona i raczej powinniśmy dążyć do zwiększenia jej złożoności niż do zmniejszenia, bo dzięki temu będzie ona w stanie wychwycić więcej cech obrazka. Zmniejszając złożoność architektury, warto więc w pierwszym ruchu ograniczyć złożoność części gęsto połączonej. 

Z modelu podsieci gęsto połączonej w postaci:

Dense(units=512, activation="relu"),
Dense(units=64, activation="relu"),
Dense(units=10, activation="softmax")

przejdziemy do dużo prostszego:

Dense(units=32, activation="relu"),
Dense(units=16, activation="relu"),
Dense(units=10, activation="softmax")

(...)
>>> Epoch 78/80
>>> loss: 0.5725 - accuracy: 0.7968 - val_loss: 0.7897 - val_accuracy: 0.7367
>>> Epoch 79/80
>>> loss: 0.5667 - accuracy: 0.8014 - val_loss: 0.8373 - val_accuracy: 0.7259
>>> Epoch 80/80
>>> loss: 0.5611 - accuracy: 0.8019 - val_loss: 0.8255 - val_accuracy: 0.7220

eval = model.evaluate(x_test, to_categorical(y_test))
>>> loss: 0.8427 - accuracy: 0.7164

Jak widać, korzyści jest kilka. O około 2% wyższa skuteczność klasyfikacji na zbiorze testowym. Szybsze uczenie, bo sieć jest mniej wymagająca obliczeniowo. A także zmniejszony, choć nie wyeliminowany, overfitting – obecnie na poziomie około 10%.

Architektura naszej pierwszej wersji sieci, zaproponowana w części drugiej tutoriala, zakładała przetworzenie każdego obrazka przez trzy „moduły” konwolucyjne, z odpowiednio: 64, 32 i 16 filtrami. Taka złożoność sieci konwolucyjnej pozwoliła na uzyskanie około 80% skuteczności klasyfikacji na zbiorze treningowym, co przełożyło się na ~72% na zbiorze testowym. Dla przypomnienia wyglądała ona tak:

Convolution2D(filters=64, kernel_size=(3,3), input_shape=(32,32,3), activation='relu', padding='same'),
Convolution2D(filters=64, kernel_size=(3,3), activation='relu', padding='same'),
MaxPool2D((2,2)),
Convolution2D(filters=32, kernel_size=(3,3), activation='relu', padding='same'),
Convolution2D(filters=32, kernel_size=(3,3), activation='relu', padding='same'),
MaxPool2D((2,2)),
Convolution2D(filters=16, kernel_size=(3,3), activation='relu', padding='same'),
Convolution2D(filters=16, kernel_size=(3,3), activation='relu', padding='same'),

Abyśmy mogli uzyskać lepsze rezultaty klasyfikacji, powinniśmy poprawić wyniki w dwóch obszarach. Po pierwsze, zwiększyć poprawność klasyfikacji na zbiorze treningowym, bo jak widać skuteczność dla zbioru testowego jest zawsze niższa niż skuteczność dla zbioru uczącego. Po drugie, powinniśmy zmniejszyć overfitting. Sieć, która nauczy się dobrze generalizować wyniki, osiągnie dużo lepsze wyniki na danych, których nie widziała. Poza tym będziemy w stanie uczyć ją dłużej niż przez 80 epok. Obecnie nie ma to większego sensu, bo mimo iż skuteczność na zbiorze treningowym może jeszcze urosnąć, to ten sam parametr na zbiorze walidacyjnym wskazuje, że to uczenie nie jest generalizowaniem, a dopasowaniem do zbioru uczącego.

Jak zwiększyć poprawność klasyfikacji na zbiorze treningowym? Jedną z dróg jest pogłębienie podsieci konwolucyjnej. Dodając kolejne warstwy i zwiększając ilość filtrów, dajemy możliwość wychwycenia przez sieć większej ilości cech i tym samym większej skuteczności w klasyfikacji. Aby to osiągnąć, do naszej architektury, na sam jej początek, dodamy jeszcze jeden „moduł” konwolucyjny, ze zwiększoną do 128 ilością filtrów:

Convolution2D(filters=128, kernel_size=(5,5), input_shape=(32,32,3), activation='relu', padding='same'),
Convolution2D(filters=128, kernel_size=(5,5), activation='relu', padding='same'),
MaxPool2D((2,2)),
Convolution2D(filters=64, kernel_size=(5,5), activation='relu', padding='same'),
Convolution2D(filters=64, kernel_size=(5,5), activation='relu', padding='same'),
MaxPool2D((2,2)),
Convolution2D(filters=32, kernel_size=(5,5), activation='relu', padding='same'),
Convolution2D(filters=32, kernel_size=(5,5), activation='relu', padding='same'),
MaxPool2D((2,2)),
Convolution2D(filters=16, kernel_size=(3,3), activation='relu', padding='same'),
Convolution2D(filters=16, kernel_size=(3,3), activation='relu', padding='same'),

Próba zmniejszenia overfittingu wymaga wprowadzenia dwóch nowych elementów: normalizacji batchowej (batch normalization) i techniki dropout.

Normalizacja batchowa

Normalizacja batchowa ma na celu redukcję tzw. internal covariate shift. Aby zrozumieć ideę stojącą za normalizacją batchową, należy uprzednio zrozumieć, czym jest internal covariate shift.

Covariate jest dość szeroko używanym terminem, głównie w statystyce, i oznacza zmienną niezależną, czyli innymi słowy zmienną wejściową. Na podstawie zmiennych wejściowych wyznacza się zmienne zależne – wyjściowe. Przez analogię, w uczeniu maszynowym covariate będzie oznaczał zmienną wejściową / input / X / features. W naszym przykładzie covariate to wartości składowych kolorów poszczególnych pikseli przetwarzanych obrazków.

Każdy zbiór danych posiada pewną dystrybucję / rozkład danych wejściowych. Dla przykładu, gdybyśmy w zbiorze CIFAR-10 analizowali rozkład średniej jasności obrazków przedstawiających samoloty, zapewne byłby on różny od jasności obrazków przedstawiających żaby. Gdybyśmy nałożyli na siebie takie dwa rozkłady, to byłyby one względem siebie przesunięte. To przesunięcie nazywamy covariate shift.

Mimo że zbiory danych, których używamy do uczenia maszynowego są z reguły dobrze zbilansowane, to jednak podział zbioru na uczący, walidacyjny i testowy powoduje, że zbiory te mają różny rozkład danych wejściowych. Z tego też (między innymi) powodu mamy do czynienia z niższą skutecznością wyuczonej sieci dla zbioru testowego, w porównaniu do zbioru uczącego.

Covariate shift występuje nie tylko przy podziale zbioru lub przy jego wzbogacaniu o nowe dane, ale również w wyniku przechodzenia danych wejściowych przez kolejne warstwy sieci neuronowej. Sieć modyfikuje dane w naturalny sposób, poprzez nakładanie wag przypisanych do połączeń między neuronami w sieci. W konsekwencji każda kolejna warstwa musi się nauczyć danych, które mają nieco inny rozkład niż oryginalne dane wejściowe. Powoduje to nie tylko spowolnienie procesu uczenia, ale również większą podatność sieci na overfitting. Zjawisko przesunięcia rozkładu danych wejściowych w sieci neuronowej zostało opisane przez Ioffe oraz Szegedy i nazwane internal covariate shift.

Ioffe i Szegedy zaproponowali metodę normalizacji danych wykonywaną pomiędzy warstwami sieci neuronowej, jako część jej architektury, dzięki czemu można zminimalizować zjawisko internal covariate shift. Należy tu zauważyć, że niektórzy naukowcy zajmujący się zagadnieniem wskazują, że normalizacja batchowa nie tyle redukuje internal covariate shift, co raczej wygładza funkcję celu, dzięki czemu przyspiesza i poprawia proces uczenia.

Podsumowując: normalizacja batchowa przyspiesza uczenie – pozwala przy mniejszej liczbie iteracji uzyskać takie same rezultaty jak sieci nieposiadające normalizacji batchowej. Umożliwia zastosowanie wyższych learning rates bez negatywnego wpływu na gradienty oraz pomaga również eliminować overfitting. Większość bibliotek uczenia maszynowego, w tym keras, posiada wbudowane funkcje realizujące normalizację batchową.

Dla zainteresowanych: wpis na wiki oraz artykuł naukowy Sergeya Ioffe i Christiana Szegedy, którzy zaproponowali i opisali metodę normalizacji batchowej. Artykuł jest mocno techniczny, z dużą dawką matematyki, ale abstrakt, wprowadzenie i podsumowanie są całkiem zjadliwe. 😉

Dropout

Drugą bardzo przydatną techniką, która skutecznie walczy z overfittingiem jest tzw. dropout. Zaproponował ją Geoffrey E. Hinton et al. w pracy Improving neural networks by preventing co-adaptation of feature detectors. Jest to relatywnie prosta, ale zarazem bardzo skuteczna technika przeciwdziałania overfittingowi. Polega na losowym usuwaniu z sieci (z warstw wewnętrznych, czasami również wejściowych) pojedynczych neuronów w trakcie uczenia. Ponieważ skomplikowane sieci (a takie niewątpliwie są głębokie sieci neuronowe), szczególnie dysponujące relatywnie niewielkimi ilościami danych uczących, mają tendencję do dokładnego dopasowywania się do danych, to taki sposób deregulacji zmusza je do uczenia w sposób bardziej zgeneralizowany.

W każdej turze uczenia się każdy z neuronów jest usuwany lub zostawiany w sieci. Szanse na usunięcie definiuje się poprzez określenie prawdopodobieństwa, z jakim neuron zostanie usunięty. W oryginalnej pracy było to 50% dla każdego neuronu. Obecnie możemy samodzielnie określić to prawdopodobieństwo, a do tego dla różnych warstw może być ono różne.

Zastosowanie dropout w praktyce prowadzi do sytuacji, w której architektura sieci zmienia się dynamicznie i otrzymujemy model, w którym jeden zbiór danych został wykorzystany do nauczenia wielu sieci o różniących się architekturach, a następnie został przetestowany na zbiorze testowym z uśrednionymi wartościami wag.

Użycie dropout w Keras sprowadza się do dodania kolejnej warstwy o nazwie Dropout(rate), której hiperparametrem jest prawdopodobieństwo, z jakim neuron zostanie usunięty z sieci. Dropout dodajemy do podsieci gęsto połączonej. Użycie jej w podsieci konwolucyjnej jest rzadsze i w zasadzie mija się z ideą stojącą za konwolucjami.

W warstwie konwolucyjnej zastosujemy natomiast normalizację batchową, którą w Keras uzyskujemy poprzez dodanie warstwy BatchNormalization(). W efekcie otrzymamy następującą architekturę sieci:

optim = RMSprop(lr=0.001)

Jak widać powyżej, zaproponowałem również zmianę optymalizatora z SGD na RMSprop, który jak wynikało z moich testów sprawdził się nieco lepiej dla powyższej architektury.

W tym miejscu mała dygresja: możecie zastanawiać się, skąd są te wszystkie zaproponowane przeze mnie zmiany? No cóż, płyną one z dwóch źródeł: z zebranych doświadczeń oraz eksperymentów z daną siecią. Nad rozwiązaniem, które ostatecznie zaprezentuję w niniejszym tutorialu, spędziłem co najmniej kilkanaście godzin, próbując różnych architektur i wartości hiperparametrów. Tak to wygląda w praktyce, więc jeżeli spędzacie ze swoim modelem drugi dzień i nie macie pojęcia co dalej, to musicie wiedzieć, że jest to całkowicie normalne i za chwilę (lub po małej przerwie) pójdziecie zapewne z pracą dalej.

Sieć była uczona 80 epok i w efekcie uzyskaliśmy skuteczność klasyfikacji na poziomie 81%.

Epoch 77/80
42500/42500 - 19s - loss: 0.0493 - accuracy: 0.9888 - val_loss: 1.7957 - val_accuracy: 0.8119
Epoch 78/80
42500/42500 - 19s - loss: 0.0523 - accuracy: 0.9879 - val_loss: 1.2465 - val_accuracy: 0.8016
Epoch 79/80
42500/42500 - 19s - loss: 0.0499 - accuracy: 0.9880 - val_loss: 1.7057 - val_accuracy: 0.8137
Epoch 80/80
42500/42500 - 18s - loss: 0.0490 - accuracy: 0.9880 - val_loss: 1.5880 - val_accuracy: 0.8175

eval = model.evaluate(x_test, to_categorical(y_test))
>>> 10000/10000 [==============================] - 2s 167us/sample - loss: 1.5605 - accuracy: 0.8112

Rzut oka na wykresy dla zbioru uczącego i walidacyjnego dają mieszane uczucia. Z jednej strony udało nam się podnieść skuteczność klasyfikacji dla wszystkich trzech zbiorów, w tym dla najważniejszego, czyli testowego o blisko 10% (z 71% do 81%). Z drugiej strony znowu pojawił się silny overfitting, co oznacza, że sieć ponownie bardziej „uczy się zbioru treningowego” niż generalizuje klasyfikację.

Gdybym chciał w tej chwili uzyskać istotnie lepszy wynik klasyfikacji niż 81%, to wybrałbym jedną z trzech dróg. Po pierwsze, można byłoby poeksperymentować z inną architekturą. W tym można byłoby sięgnąć do jednej z referencyjnych architektur, które uzyskiwały bardzo dobre rezultaty na zbiorze CIFAR-10 lub podobnych. Po drugie, należałoby zbadać reakcję naszej sieci na inne ustawienia hiperparametrów – praca żmudna i wymagająca czasu, ale czasami kilka prostych zmian daje dobre rezultaty. Trzecią drogą jest dalsza walka z overfittingiem, ale nieco inną metodą, o której już wspominałem powyżej – data augmentation. Przyjrzymy się jej w kolejnej części tutoriala.

Konwolucyjne sieci neuronowe – kilka praktycznych porad

Na sam koniec części trzeciej tutoriala zamieszczam kilka praktycznych, luźno powiązanych porad, które można uwzględnić, budując swoją konwolucyjną sieć neuronową.

• Jeżeli możesz, skorzystaj ze sprawdzonej architektury sieci i w miarę możliwości dostosuj ją do swoich potrzeb.
• Zacznij od overfittingu i wprowadź regularyzację.
• Umieszczaj dropout w warstwie gęsto połączonej, a normalizację batchową wprowadź do podsieci konwolucyjnej. Nie trzymaj się jednak sztywno tej zasady. Czasami niestandardowy ruch może dać niespodziewanie dobre efekty.
• Kernel size powinien być raczej dużo mniejszy niż rozmiar obrazka.
• Eksperymentuj z różnymi ustawieniami hiperparametrów, a potem eksperymentuj jeszcze więcej.
• Korzystaj z GPU. Jeżeli nie masz komputera z odpowiednią kartą graficzną, skorzystaj z Google Colaboratory.
• Zgromadź tyle danych uczących, ile to możliwe. Nie ma czegoś takiego jak „za dużo danych”.
• Jeżeli nie możesz zgromadzić większej ilości danych, skorzystaj z generatora danych – więcej o tym w czwartej części tutoriala.
• Bardzo głęboka i rozbudowana sieć będzie miała silne skłonności do overfittingu. Skorzystaj z tak płytkiej sieci, jak to możliwe. W szczególności nie przesadzaj z ilością neuronów i warstw w podsieci gęsto połączonej.
• Upewnij się, że zbiory uczące i testowe są dobrze zbalansowane i mają zbliżoną dystrybucję. W przeciwnym wypadku na zbiorze testowym będziesz zawsze uzyskiwał dużo gorsze wyniki niż na zbiorze uczącym.
• Jak już poczujesz się dobrze w świecie Convnetów, zacznij czytać bardziej zaawansowane opracowania naukowe. Pozwolą Ci lepiej zrozumieć jak działają sieci konwolucyjne, wprowadzą do Twojego arsenału nowe techniki i architektury.

Powodzenia i zapraszam do czwartej części tutoriala.

---

Masz pytanie? Zadaj je w komentarzu.

Spodobał ci się post? Będzie mi miło, gdy go polecisz.

Do zobaczenia wkrótce, przy okazji omawiania innego ciekawego tematu!

---

Czy oglądasz mecze NBA? Sprawdź mój darmowy serwis NBA Games Ranked i ciesz się oglądaniem wyłącznie dobrych meczów.

---