Neuronowe sieci konwolucyjne 2: architektura

Neuronowe sieci konwolucyjne pozwalają uzyskać bardzo dobre wyniki klasyfikacji w przypadku obrazów. W poprzednim poście mieliście okazję dowiedzieć się, czym jest konwolucja oraz jak sklasyfikować zbiór CIFAR-10 wykorzystując prostą klasyczną sieć neuronową. Przypomnę, że uzyskaliśmy poprawność klasyfikacji na zbiorze testowym na poziomie 47%.

W drugiej części tutoriala idziemy dalej:

• wyjaśniamy podstawowe pojęcia i architekturę neuronowych sieci konwolucyjnych,
• budujemy prostą sieć konwolucyjną i sprawdzamy jak radzi sobie ona na zbiorze CIFAR-10,
• wstępnie wyjaśniamy czym jest overfitting – zagadnienie, z którym będziemy mierzyli się w części trzeciej.

Niniejszy post jest drugą częścią tutoriala, więc jeżeli nie czytaliście części pierwszej, zapraszam najpierw do jej lektury.

Neuronowe sieci konwolucyjne – architektura

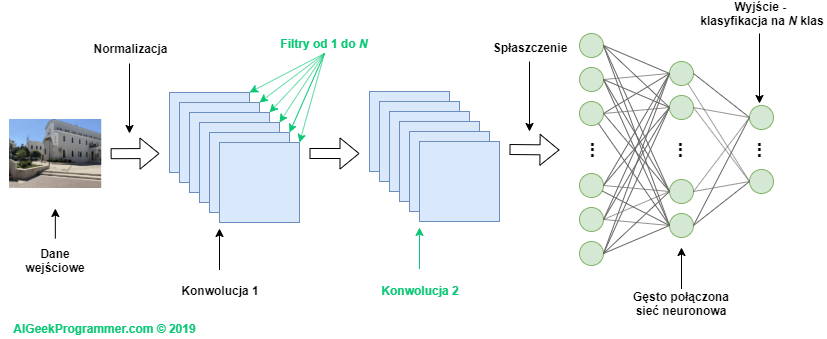
Zacznijmy od tego, że sieć konwolucyjna składa się de facto z dwóch podsieci. Pierwsza z nich dokonuje konwolucji tensora wejściowego. Druga jest klasyczną, gęsto połączoną siecią neuronową, zakończoną warstwą, która klasyfikuje dane wejściowe na N klas – jak w przykładzie z pierwszej części tutoriala.

Podsieć konwolucyjna wykorzystuje z reguły dane trójwymiarowe, czyli nieprzetworzone (poza ich normalizacją). Sieć neuronowa wymaga natomiast danych spłaszczonych do jednego wymiaru. Przyjmując taki nieco sztuczny podział na podsieci i wiedząc z pierwszej części tutoriala oraz z innych moich postów, jak klasyfikować dane z wykorzystaniem klasycznej sieci neuronowej, możemy się w zasadzie skupić na pierwszym elemencie, czyli podsieci konwolucyjnej.

Zanim wejdziemy głębiej w architekturę sieci konwolucyjnej, zastanówmy się przez chwilę dlaczego dobrze radzą sobie one z obrazkami? Jeżeli czytaliście mój post o klasyfikacji pisma odręcznego, to być może pamiętacie, że wszystkie cyfry były mniej więcej w centrum obrazka. Wyglądało to tak:

Sieć neuronowa dobrze radziła sobie z klasyfikacją, mając gwarancję, że to, co najbardziej interesujące znajdzie się zawsze w centrum obrazka.

Co jednak, jeśli cyfra byłaby przesunięta w którąś stronę?

Prawdopodobnie klasyczna sieć neuronowa, w dodatku wyuczona na centralnie umiejscowionych cyfrach, nie byłaby w stanie poradzić sobie z takimi danymi. W języku angielskim istnieje termin „translational invariance” – dosłownie „niezmienność tłumaczenia”. Lepiej i zdecydowanie bardziej sensownie według mnie brzmi „niewrażliwość na zmiany położenia”. Termin ten oznacza, że potrafimy rozpoznać obiekt jako ten właściwy obiekt, nawet jeżeli jego wygląd lub położenie w pewnym stopniu uległo zmianie: poprzez przesuniecie, rotację, zmianę wielkości, kolorów, jasności, itp. Jak w przykładzie powyżej, kiedy zero przesunęliśmy w lewy górny róg, a mimo to dla ludzkiego mózgu jest to nadal bezsprzecznie zero. Dla sieci neuronowej niemającej cechy „translational invariance” będzie to obiekt inny niż zero – prawdopodobnie niemożliwy do sklasyfikowania dla sieci wyuczonej na symbolach wypośrodkowanych. Warto zauważyć, że słowo „translational” jest nieco mylące. Nie chodzi tu wcale o tłumaczenie, ale bardziej o tranzycję. Zostało wzięte z geometrii, gdzie oznacza przesunięcie każdego piksela w ten sam sposób.

ConvNety są niewrażliwe na położenie, ponieważ ich centralnym elementem jest operacja konwolucji, która polega na przetworzeniu każdego fragmentu obrazu przez tą samą wartość filtra. Innymi słowy: konwolucja nie patrzy na centrum obrazka, czy na jakikolwiek inny jego obszar. Przebiega ona filtrem przez całą jego powierzchnię, a tam gdzie akurat znajdzie jakaś interesująca cecha, w wyniku konwolucji pojawią się charakterystyczne wartości.

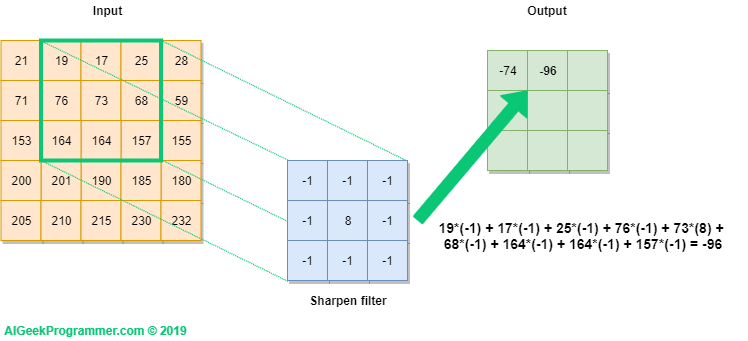
Rysunek nr 2 prezentuje w formie graficznej w jaki sposób realizujemy operację konwolucji na obrazku 5×5 pikseli, oznaczonym jako Input, wykorzystując do tego filtr o rozmiarze 3×3 i wartościach, które już pojawiły się w pierwszej części tutoriala przy okazji wyostrzania krawędzi obrazka. Filtr jest rzutowany na obrazek (zielona ramka), a następnie wartość każdego piksela obrazka jest przemnażana przez odpowiadającą mu wartość filtra. W rezultacie otrzymujemy wartość -74. Obliczenia dla ułatwienia zapisałem pod outputem.

W kolejnym kroku filtr jest przesuwany o jedną pozycję i obliczenia są powtarzane. Jako wynik otrzymujemy wartość -96.

Dla ostatniego kroku uzyskujemy wartość -43, jak pokazano na rysunku 4 poniżej.

Filtr przebiega po całym inpucie, od lewej ku prawej i z góry na dół, ostatecznie wypełniając wartościami całość outputu.

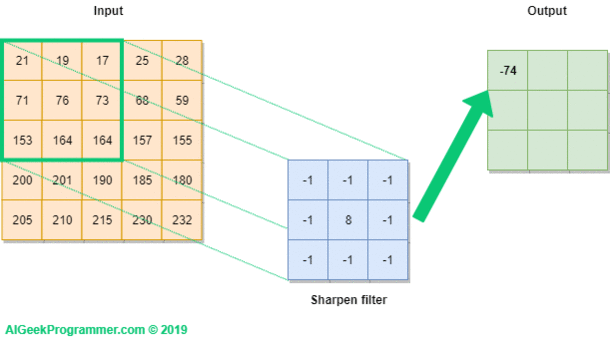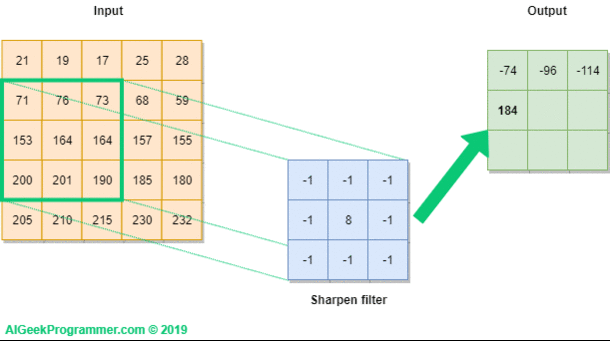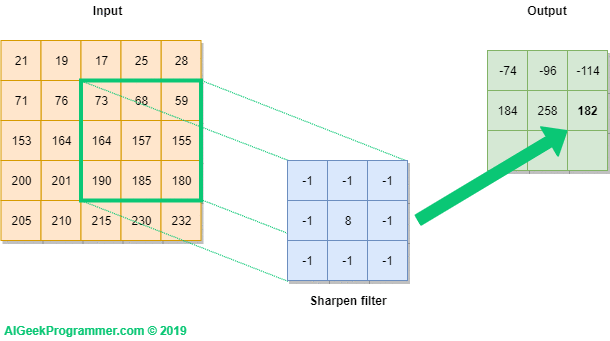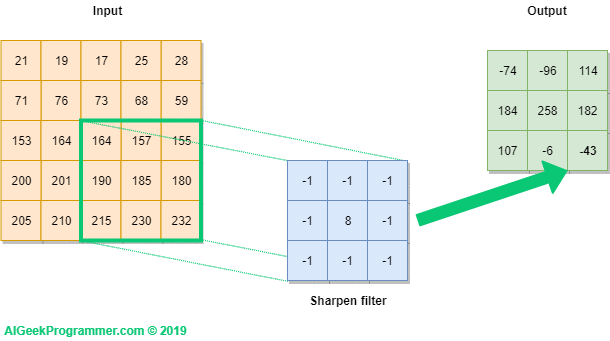
Jak widać, w wyniku konwolucji obrazka możemy uzyskać wartości zarówno poniżej zera, jak i większe niż 255. Pamiętajmy jednak, że celem konwolucji w sieci neuronowej jest detekcja cech obrazka, a nie jego wizualizacja po przetworzeniu filtrem. Stąd nie ma to w zasadzie znaczenia do momentu, kiedy chcemy wyświetlić obrazek po konwolucji (a w trakcie procesu uczenia dzieje się tak w zasadzie rzadko). W takim przypadku powinniśmy w pierwszej kolejności dokonać przesunięcia wartości, a dopiero w drugim kroku obcięcia tych powyżej 255 do 255, a tych poniżej 0 do wartości 0. Zagadnienie, o jaką wartość należy dokonać przesunięcia, jest dość skomplikowane i wykracza poza zakres tego tutoriala. Zainteresowanych odsyłam w pierwszej kolejności do tego wątku na stackoverflow.

Podsumowując, dane po konwolucji stają się niewrażliwe na położenie obiektu. Bez względu na to, gdzie będzie on zlokalizowany, konwolucja będzie w stanie go znaleźć i zwrócić dla niego charakterystyczny zestaw danych. Zestaw rozpoznawalny potem przez sieć neuronową. W tym rozumieniu ConvNety są niewrażliwe na zmiany położenia obiektu i jest to jeden z głównych powodów, dla których tak doskonale radzą sobie z klasyfikacją obrazów.

Podobnie jak podsieć neuronowa, podsieć konwolucyjna może być wielowarstwowa. Oznacza to, że każda kolejna warstwa jest w stanie znaleźć kolejne właściwości obrazka (z ang. features).  Co więcej, każda warstwa konwolucji również jest wielowymiarowa, bo dla każdej warstwy definiuje się N filtrów (patrz rysunek 6). Wartości filtrów są różnie zainicjowane dla każdego z nich i mogą one dzięki temu lepiej lub gorzej znajdować cechy obrazka istotne dla poprawnej klasyfikacji. Algorytm propagacji wstecznej będzie obniżał istotność filtrów nieskutecznych, a promował te wspomagające prawidłową klasyfikację. Stąd po wielu, wielu iteracjach będziemy dysponowali zestawem skutecznych filtrów. Skutecznych – w znaczeniu pomagających sieci poprawnie klasyfikować obrazek, a ostatecznie poprawnie generalizować proces klasyfikacji.

 

Innym istotnym elementem Convnetów jest wykonywanie tzw. operacji maxpoolingu. Czym jest maxpooling również najlepiej wyjaśnić jest graficznie.

Analizujemy wartości czterech sąsiadujących pikseli, wybieramy wartość największą i ona staje się wyjściem/wynikiem operacji. W kolejnym kroku okno operacji przesuwamy na następną grupę pikseli i powtarzamy obliczenia. W przeciwieństwie do konwolucji okna wykonywania maxpoolingu nie nachodzą na siebie. Stąd w naszym przykładzie kolejnym oknem będą piksele: 114, 105, 182 oraz 75.

Maxpooling możemy również wykonać na większej próbce np. 3×3, 4×4, itd. Warto zwrócić uwagę, że maxpooling o wielkości M x M redukuje wymiar obrazka o M². Czyli obrazek 32 x 32 (1024 piksele), po wykonaniu maxpoolingu 2×2 będzie miał wymiar 16×16 = 256 pikseli, czyli 2² mniej.

W jakim celu wykonujemy maxpooling? Główny powód poznaliście już powyżej. Następuje redukcja wymiarowości i to bez utraty informacji istotnych dla klasyfikacji, dzięki czemu problem upraszcza się obliczeniowo. Po wykonaniu konwolucji (tu w znaczeniu: po nałożeniu filtra na dany obszar obrazka) interesuje nas jedynie, czy istotna cecha została w danym obszarze znaleziona czy nie. Nie interesuje nas każda pojedyncza wartość piksela po konwolucji, a tylko te wartości, które dają silną odpowiedź (wskazówkę) naszej sieci. Dlatego patrzymy na wartości sąsiadujących pikseli i wybieramy z nich wartość największą – najbardziej istotną. Dodatkowo, maxpooling pomaga zidentyfikować te elementy obrazka, które są najbardziej widoczne. Dzięki temu osiągamy również wyższy poziom „translational invariance”.

Poza operacją maxpoolingu są jeszcze operacje average poolingu (zamiast wartości maksymalnej wyliczamy średnią) i minpoolingu, ale nie znajdują one szerokiego zastosowania w Convnetach.

Wymiarowanie sieci konwolucyjnych

Jak być może zwróciliście uwagę podczas oglądania rysunków od 2 do 5, operacja konwolucji na obrazku o rozmiarze 5×5, filtrem 3×3 dała w efekcie nowy „obrazek” o wielkości 3×3. Stąd prosty wniosek, że konwolucja może zmieniać wymiary przetwarzanych danych i warto zrozumieć, w jaki sposób wymiary te się zmieniają oraz jak te zmiany kontrolować. Ponieważ na blogu staram się korzystać z API biblioteki Keras, to za przykład posłuży mi linia kodu, którą zobaczymy później, a która definiuje parametry jednej z warstw konwolucyjnych:

Convolution2D(filters=32, kernel_size=(3,3), activation='relu',padding='same')

Powyższy kod tworzy warstwę konwolucyjną mającą 32 filtry, każdy o wymiarze 3×3, a wyjście z warstwy dodatkowo przechodzi przez funkcję aktywacji relu. Dla omawianego problemu istotna jest opcja padding, tu ustawiona na wartość same, co oznacza, że po konwolucji obrazek będzie miał niezmienioną wielkość. Jak to możliwe? Jak sama nazwa sugeruje używamy do tego sztucznie dodanego marginesu (paddingu), wypełnionego zerami. Keras i Tensorflow oferują dwa sposoby obsługi marginesów: same i valid.

Tryb valid widzieliśmy na przykładach pokazanych na rysunkach od 2 do 5. Filtr nie wychodzi wówczas poza obszar obrazka i co za tym idzie, obrazek wyjściowy jest mniejszy. Jest na to nawet prosty wzór. Jeżeli obrazek ma wielkość D x D (w naszym przykładzie 5 x 5), a filtr jest wielkości N x N (tu: 3 x 3), to wielkość wynikowego obrazka wyliczymy ze wzoru: D – N + 1. Dla naszego przykładu będzie to 5 – 3 + 1 = 3.

Tryb same zachowuje wielkość obrazka po przetworzeniu przez konwolucję. Zatem wejście i wyjście z warstwy konwolucji będzie tej samej wielkości. Aby to osiągnąć, Keras i inne frameworki dobierają wielkość marginesu, tak aby filtr przeszedł po obrazku z marginesem tyle razy, ile wynosi wymiar obrazka wejściowego. W naszym przypadku do obrazka o wymiarach 5 x 5 Keras doda po jednym pikselu marginesu (paddingu).

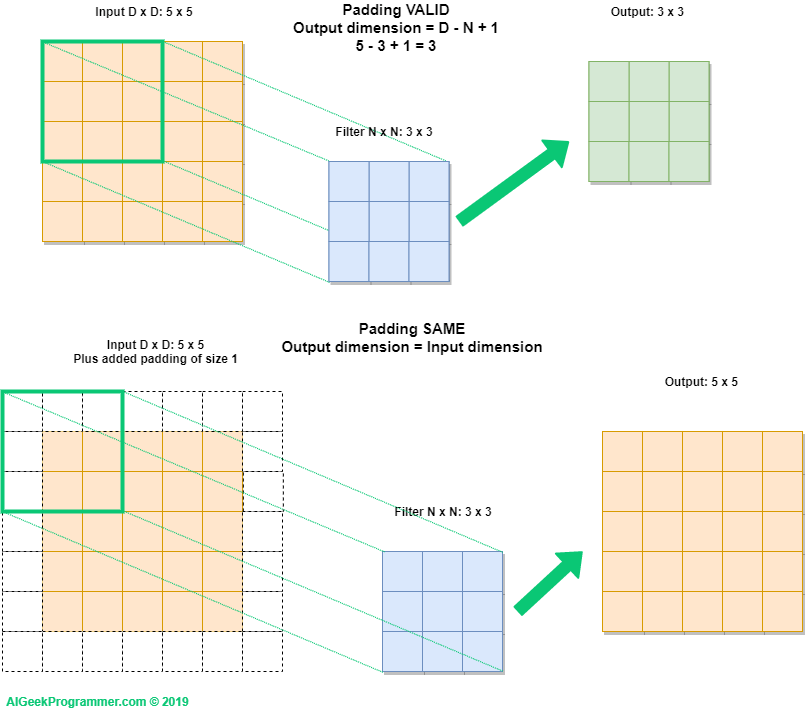
Warto dodać, że dla małych obrazków – takich jak w zbiorze CIFAR-10 – warto stosować padding = „same”, aby wielkość obrazka wyjściowego z konwolucji nie spadła za szybko, bo wówczas nie będziemy mieli możliwości dodania drugiej i kolejnych warstw konwolucyjnych lub wykonania maxpoolingu.

Przykład wymiarowania

Na podstawie tego, czego dowiedzieliśmy się powyżej, spróbujmy prześledzić wymiary w prostej sieci konwolucyjnej. Załóżmy, że będzie się ona składała z 3 operacji konwolucji, dwóch operacji maxpoolingu oraz dwóch klasycznych warstw, gęsto połączonych. Ponadto:

1. Conv1: padding = „valid”, rozmiar filtra: 5×5, ilość filtrów: 16
2. Maxpool1: 2×2
3. Conv2: padding = „same”, rozmiar filtra: 3×3, ilość filtrów: 8
4. Maxpool2: 2×2
5. Conv3: padding = „valid”, rozmiar filtra: 3×3, ilość filtrów: 4
6. Dense1: ilość neuronów na wyjściu: 50
7. Dense2: ilość neuronów na wyjściu: 10 (klasyfikujemy na 10 klas)

Zakładając, że na wejściu mamy obrazek ze zbioru CIFAR-10, jak będą zmieniały się rozmiary?

1. Conv1: obrazek ma rozmiar 32x32x3 i wykonujemy na nim konwolucję filtrem 5×5 w trybie valid. Tu należy zauważyć, że filtr 5×5 jest nakładany na każdy kanał koloru i sumowany. Rozmiar tensora wynikowego będzie zatem 32-5+1 = 28×28. Filtrów jest 16. Stąd wyjściem z Conv1 będzie tensor o wymiarze 28x28x16.
2. Maxpool1: zmniejszy dwukrotnie rozmiar każdego z wymiarów. Stąd wyjściem z tej warstwy będzie tensor 14x14x16.
3. Conv2: w tej warstwie wykonujemy konwolucję w trybie same, a więc nie zmieni ona wymiarów obrazka. Filtrów jest 8. Stąd wyjściem z Conv2 będzie tensor o wymiarze 14x14x8.
4. Maxpool2: zmniejszy dwukrotnie rozmiar każdego z wymiarów. Stąd wyjściem z tej warstwy będzie tensor 7x7x8.
5. Conv3: wykonujemy konwolucję w trybie valid, filtrem 3×3. Rozmiar tensora wynikowego będzie zatem 7-3+1 = 5×5. Filtry są 4. Stąd wyjściem z Conv3 będzie tensor o wymiarze 5x5x4.
6. Dense1: aby przejść do klasycznej podsieci neuronowej musimy dane spłaszczyć. W efekcie otrzymamy wektor o wymiar 5*5*4 = 100. Będzie on wejściem do pierwszej warstwy podsieci neuronowej. Ma ona na wyjściu 50 neuronów i taki będzie rozmiar wektora wejściowego do ostatniej warstwy.
7. Dense2: na wejściu otrzymuje daną o rozmiarze 50, na wyjściu ma 10 neuronów, które klasyfikują wynik funkcją softmax.

Neuronowe sieci konwolucyjne – klasyfikacja zbioru CIFAR-10

Myślę, że wystarczy już tej teorii. 😉 Jesteśmy gotowi, aby spróbować zbudować prostą sieć konwolucyjną i sklasyfikować z jej użyciem zbiór CIFAR-10. Zobaczymy czy uda nam się pobić poprzedni wynik (47%), uzyskany z wykorzystaniem klasycznej sieci neuronowej. A jeśli tak, to o ile.

Do prac użyję tym razem środowiska Google Colaboratory, gdzie mamy łatwy dostęp do procesora GPU.

Ponieważ chcę skorzystać z tensorflow 2.x, a w dniu pisania posta (grudzień 2019) domyślną wersją w Colab jest nadal 1.x, to poza standardowymi importami, w notebooku należy dodać wskazanie na oczekiwaną wersję biblioteki Tensorflow:

import numpy as np

%tensorflow_version 2.x
import tensorflow

import matplotlib.pyplot as plt
%matplotlib inline
>>> TensorFlow 2.x selected.

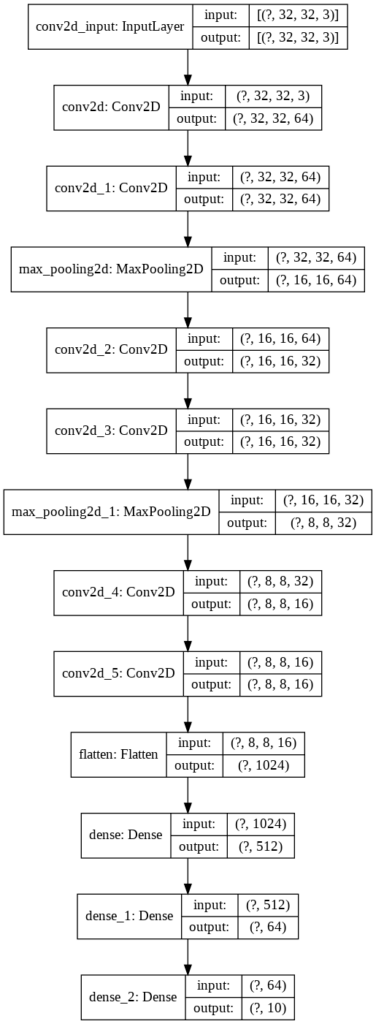
Pozostało nam ustalić optymalizator, funkcję straty i metryki, które chcemy gromadzić w trakcie uczenia. Zarówno rodzaj optymalizatora, jak i jego parametry – tu learning rate i momentum – są hiperparametrami modelu. Mogą wpływać na jego zachowanie, szybkość oraz skuteczność uczenia. To oczywiście jedne z wielu hiperparametrów naszej sieci. Sama architektura i złożoność modelu ma już zasadnicze znaczenie dla efektywności sieci. Wielkość filtrów, ich ilość, rodzaj paddingu, funkcje aktywacji, sposób normalizacji danych, rozmiar maxpoolingu – to kolejne parametry. Liczba kombinacji jest naprawdę duża. Warto skorzystać z porad, jakich jest wiele w internecie, i wystartować z parametrami, które ktoś już kiedyś sprawdził i to z dobrymi efektami, a następnie próbować eksperymentalnie poprawiać wyniki.

optim = SGD(lr=0.001, momentum=0.5)
model.compile(optimizer=optim, loss='categorical_crossentropy', metrics=['accuracy'])

Po skompilowaniu modelu możemy wystartować z procesem uczenia. Przy zadanych poniżej parametrach potrwa on od kilku do kilkudziesięciu minut (w wariancie bez GPU). Zwróćcie uwagę, że wynik działania metody fit zwracany jest do obiektu history, który będzie gromadził dane, dzięki czemu będziemy mogli zaprezentować przebieg procesu uczenia. Do metody fit dodałem również parametr validation_split, który określa, jaka część danych uczących jest zarezerwowana na proces walidacji. Proces ten odbywa się po każdej epoce, pokazując jakie efekty proces uczenia na zbiorze treningowym daje na zbiorze walidacyjnym (którego sieć nie widziała w trakcie uczenia się w tej epoce).

history = model.fit(
   x_train,
   to_categorical(y_train),
   epochs=80,
   validation_split=0.15,
   verbose=1
)

Ostateczna weryfikacja odbywa się na zbiorze testowym, którego sieć uprzednio nie widziała:

eval = model.evaluate(x_test, to_categorical(y_test))
eval
>>> [1.6473742815971375, 0.6954]

Jak widać, dzięki użyciu sieci konwolucyjnej udało nam się zwiększyć poprawność klasyfikacji z 47% do blisko 70%.

Ciekawe rzeczy można zaobserwować korzystając z danych zebranych w obiekcie history:

plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper left')
plt.show()

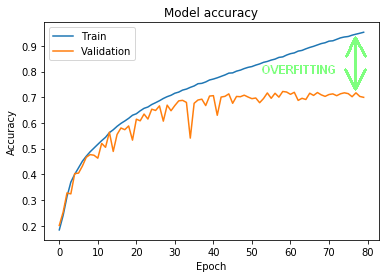
Na rysunku 10. mamy zaprezentowane wyniki uczenia na zbiorze treningowym (linia niebieska) oraz wynik na zbiorze walidacyjnym (linia pomarańczowa). Jak widać, już w okolicach 15 epoki oba zbiory zaczęły uzyskiwać inne wyniki. Poprawność klasyfikacji zbioru uczącego stopniowo rosła do samego końca, osiągając pod koniec wartości w okolicach 95%. Tymczasem walidacja poradziła sobie dużo gorzej. Tak samo zbiór testowy.

Co to oznacza? Otóż mamy tu do czynienia ze zjawiskiem overfittingu (oznaczonym przeze mnie na rysunku 10. zieloną strzałką): sieć w procesie nauki doskonale nauczyła się rozpoznawać obiekty ze zbioru uczącego, ale nie potrafiła zgeneralizować nauki w taki sposób, aby równie poprawnie klasyfikować obiekty uprzednio niewidziane. Nie jest to dobra wiadomość, bo sieć nie poradzi sobie dobrze z danymi spoza procesu nauki. Na szczęście jest kilka technik, które zmniejszają overfitting – zajmiemy się nimi w trzeciej części tutoriala.